Estimando o desempenho do Embraer-145LR
Estimando a perfomance de um Embraer 145LR com base em parâmetros geométricos gerais.
1. Uma breve história sobre o EMB-145
A evolução do mercado no final dos anos 1980 provocou discussões acaloradas sobre os novos conceitos usados na aviação regional. Os passageiros demonstravam uma aversão cada vez maior aos turboélices, exatamente quando crescia a demanda por viagens regionais de curta distância. Uma Nova Era, era marcada por motores a jato, surgia no Horizonte.
Em 1989, a Embraer decidiu entrar no mercado relativamente novo, mas em rápido crescimento, de jatos regionais. Essa decisão revelou-se um passo estratégico decisivo, uma vez que o mercado para suas aeronaves turboélices encontrava-se numa fase de declínio que só fez se afundar nos anos subsequentes. Os jatos têm a capacidade de voar a velocidades maiores e acima da turbulência, proporcionando maior conforto para os passageiros. A Comair, empresa baseada nos Estados Unidos e importante operadora do EMB 120, contratou a Embraer para discutir a possibilidade de operar um jato na faixa de 50 passageiros. A Embraer respondeu ao chamado do mercado, por aviões maiores e mais rápidos acionados por motores turbofan e caracterizados por custos operacionais mais baixos, lançando o EMB 145, mais tarde denominado RJ 145. O avião surgiu pela primeira vez nas pranchetas do desenho da Embraer em 1988, durante o período do desenvolvimento do CBA 123.
Em seu conceito original, RJ-145 era uma versão a jato do Brasília ampliado para acomodar 45 lugares em vez de 30 passageiros. Os desenhos iniciais previam a instalação de turbinas em baixo de cada uma das asas em substituição aos motores turboélices do Brasília. O jato poderia ser equipado quer com sistema aviônico padrão do Brasília quer com aviônica totalmente digital do high tech CBA 123.
Projetista e engenheiros esperavam reduzir os custos lançando mão da estrutura e de componentes comuns aos 2 aviões o que também permitiria potencialmente acelerar a produção. Os custos de produção para o novo jato foram estimados em USS 300 milhões. Testes desenvolvidos no túnel de vento na sede da Boeing revelaram que o RJ 145 segundo suas especificações originais jamais satisfaria os objetivos da Embraer de modo que a companhia decidiu redesenhar aeronave. Uma asa totalmente nova foi projetada e o motor a jato foi deslocado para baixo da asa como no Boeing 737.
Essas modificações, contudo, revelaram ser insuficientes. O projeto da aeronave teve de passar por novas modificações. Para reduzir os custos associados a necessidade de um trem de pouso maior e para acomodar as portas e escadas reprojetadas para passageiros, ao mesmo tempo em que se ampliava fuselagem para comportar essas mudanças, os projetistas optaram por deslocar os motores na fuselagem posterior, próximo à cauda como no Sud Aviation SE 210 Caravelle e no Boeing 727. Com isso, o preço por unidade fabricada passou a ser USS 23.5 milhões.
2. Coeficiente de Arrasto Parasita ($C_{D_0}$)
As análises de desempenho de uma aeronave são baseadas na precisão do cálculo do $C_{D_0}$. O método no qual iremos calcular o arrasto parasita do EMB-145LR é baseado na técnica de acumulação, que consiste em calcular todos componentes que contribuem para o arrasto da aeronave.
No final todos os $C_{D_0}$ são somados e temos o coeficiente de arrasto parasita da aeronave global.Para o cálculo do arrasto parasita da aeronave $C_{D_0}$, comumente chamado de coeficiente de arrasto de sustentação zero, determinaremos alguns parâmetros da aeronave como o Fator de eficiência Aerodinâmica ou Oswald’s Factor ($e$), coeficiente de arrasto induzido($K$) e Razão de Aspecto($AR$) que serão utilizados no cálculo da polar de arrasto para as condições: limpa, decolagem e de pouso no decorrer desse trabalho.
2.1 Fator de Oswald ($e$)
Para determinação do fator de Oswald seguimos o método usando os parâmetros geométricos básicos conforme 1. Dessa maneira para encontrar o fator de Oswald para o EMB-145LR usamos a seguinte formulação matemática :
\(\begin{equation} e=e_{theo}\cdot k_{e,F}\cdot k_{e,D_{0}} \cdot k_{e,M} \end{equation}\) Onde :
$e_{theo}$ (Fator de Oswald Teórico para arrasto invíscido devido apenas a sustentação.)
$k_{e,F}$ (Fator de Correção para perdas na fuselagem.)
$k_{e,D_{0}}$ (Fator de Correção para arrasto viscoso devido a sustentação.)
$k_{e,M}$ (Fator de Correção para efeitos de Compressibilidade no arrasto induzido)
2.1.1 Cálculo do fator de Oswald teórico ( $e_{theo}$ )
Conforme as dimensões da aeronave EMB-145LR temos que :
Razão de Aspecto($AR$) = 7,84
Afilamento( $\lambda$ ) = 0,254
Enflexamento em 25% da corda ($\Lambda_{c/4}$)= 22.73°
\[\begin{equation} e_{theo}=\frac{1}{1+f(\lambda-\Delta\lambda)\cdot AR} \end{equation}\] \[\begin{equation} \Delta\lambda=-0,357+0,45\cdot e^{-0,0375\cdot \Lambda_{c/4}} \end{equation}\] \[\begin{equation} f(\lambda-\Delta\lambda)=0,0524(\lambda-\Delta\lambda)^{4} -0,015(\lambda-\Delta\lambda)^{3}+0,1659(\lambda-\Delta\lambda)^{2}-0,0706(\lambda-\Delta\lambda)+0,0119 \end{equation}\]Calculando-se os termos (3) e (4) e posteriormente substituindo em (2) encontramos :
$e_{theo}= 0,9844$
2.1.2 Cálculo do fator de correção para fuselagem ($k_{e,f}$)
O fator de correção para fuselagem é dado da seguinte maneira :
\[\begin{equation} k_{e,f}= 1-2\left(\frac{d_f}{b}\right)^{^2} \end{equation}\]Onde :
$d_{f}$ = Diâmetro da Fuselagem
$b$ = Envergadura da Asa
Para o EMB-145LR consideramos:
$d_{f}=2,4m$
$b=20,01m$
Substituindo os valores na equação (5) encontramos :
$K_{e,f}=0,9741$
2.1.3 Cálculo do fator de correção para Arrasto viscoso ( $k_{e,D_{0}}$ )
Para esse fator de correção usaremos a tabela abaixo, retirada em 2 :
Tabela 1: Fatores de correção para o cálculo do e.
| Categoria de Aeronave | $\dfrac{d_f}{b}$ | $k_{e,f}$ | $k_{e,D0}$ |
|---|---|---|---|
| Jato | 0,116 | 0,973 | 0,873 |
| Jato Particular | 0,120 | 0,971 | 0,864 |
| Turboélice | 0,102 | 0,979 | 0,804 |
| Aviação Geral | 0,119 | 0,971 | 0,804 |
A aeronave EMB-145LR se enquadra na categoria de aeronaves a jato, portanto usaremos :
$k_{e,D_{0}}=0,873$
Cálculo do fator de correção para efeitos de compressibilidade ( $k_{e,M}$ )
O fator de correção para efeitos de compressibilidade leva em conta o número de Mach conforme a equação abaixo: \(\begin{equation} k_{e,M}= a_{e}(\frac{M}{M_{comp}}-1)^{b_{e}}+ c_{e} \end{equation}\)
Onde :
$a_{e}=-0,00152$
$b_{e}=10,82$
$c_{e}=1$
$M_{comp}=0,3$
$M=0,6$
Fazendo as devidas substituições encontramos um valor de:
$k_{e,M}=0,9985$
Destacamos que apesar da aeronave voar em M 0,78 usamos um M 0,60 pois a inflûencia do número de Mach no fator de Oswald aumenta bastante após M 0,6, e isso traria imprecisão no cálculo estimado do fator de Oswald, a seguir mostramos como a inflûencia do número de Mach impacta sobre o fator de Oswald para o EMB-145LR, a figura abaixo indica a região onde o fator não varia com Mach, porém no regime transônico ocorre signifcativa alteração.
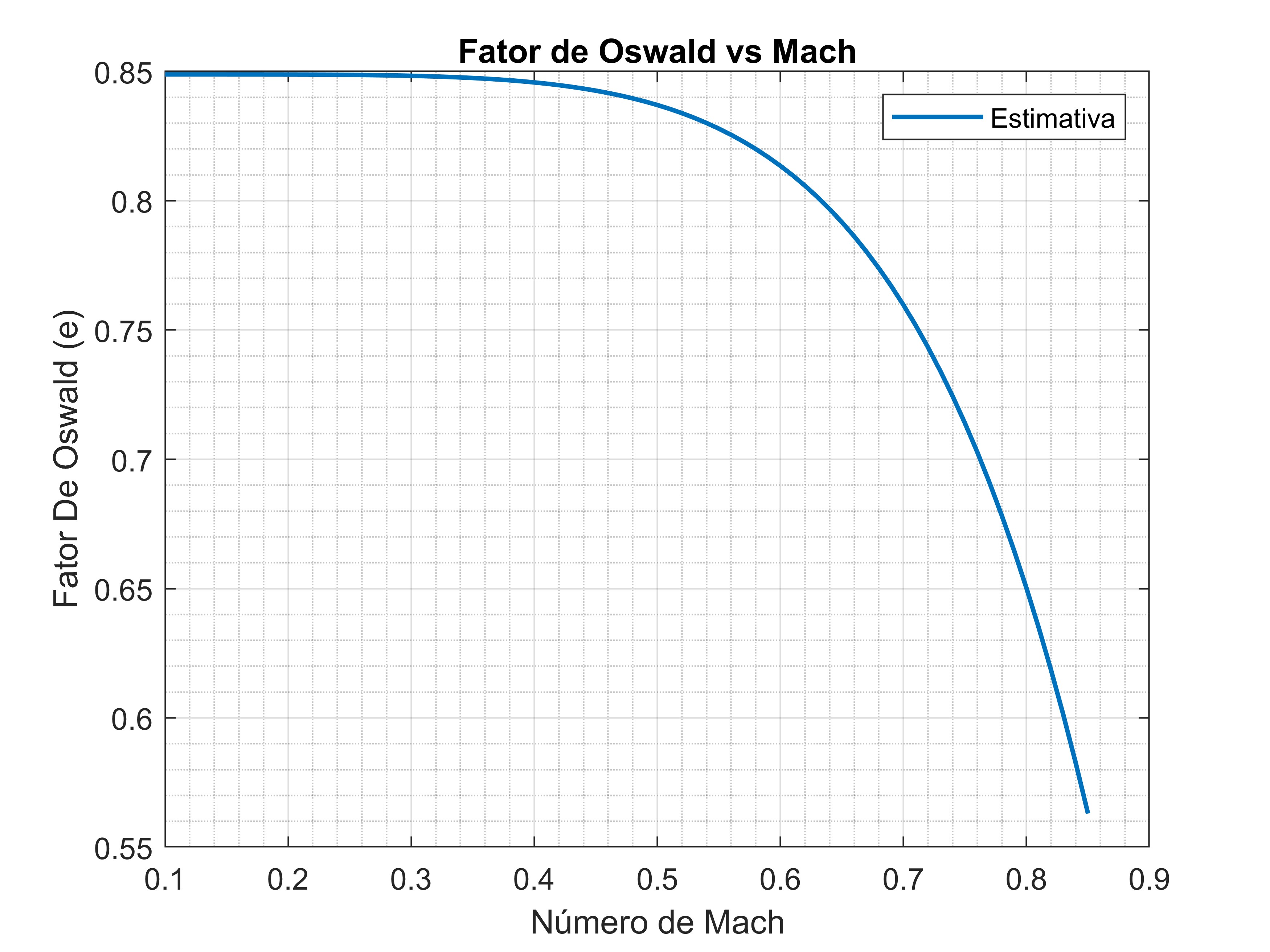Gráfico Fator de Oswald X Mach
2.1.5 Cálculo do fator de Oswald ($e$)
Após calculados os fatores de correção, usamos a equação (1) para o cálculo do fator de oswald estimado para o EMB-145LR.
\[\begin{align*} e&=e_{theo}.k_{e,F}.k_{e,D_0}.k_{e,M} \end{align*}\] \[\begin{align*} e&= 0,9844. 0,9741. 0,873. 0,9985 \end{align*}\] \[\begin{align*} e&= 0,8358\ \end{align*}\]O valor encontrado é aceitável uma vez que de acordo com 3 aeronaves com razão de aspecto entre 7 e 9 estão dentro dessa faixa de fator de Oswald.
2.2 Cálculo do Coeficiente de Arrasto Induzido ($K$)
O coficiente de arrasto induzido $K$ está associado ao arrasto induzido, sendo esse o arrasto produzido pelos componentes que geram sustentação na aeronave, sendo calculado da seguinte maneira:
\[\begin{equation} K= \frac{1}{\pi.e.AR} \end{equation}\]Substituindo os valores em (7) teremos :
\[\begin{align*} k&=\frac{1}{3,14\cdot0,8358\cdot7,84} \end{align*}\] \[\begin{align*} k&=0,0485 \end{align*}\]2.3 Cálculo do Coeficiente de Arrasto Parasita da Aeronave ($C_{D_0}$)
Conforme dito, o método utilizado para determinação do $C_{D_0}$ da aeronave será o método da acumulação, conforme a equação abaixo:
\[\begin{equation} C_{D_0}=C_{D_{0_f}}+C_{D_{0_w}}+C_{D_{0_{ht}}}+C_{D_{0_{vt}}}+C_{D_{0_{LG}}}+C_{D_{0_N}}+C_{D_{0_S}}+C_{D_{0_{HLD}}}+ ... \end{equation}\]Onde :
$C_{D_{0_f}}$ Coeficiente de arrasto parasita da Fuselagem
$C_{D_{0_w}}$ Coeficiente de arrasto parasita da Asa
$C_{D_{0_{ht}}}$ Coeficiente de arrasto parasita da Empenagem Horizontal
$C_{D_{0_{vt}}}$ Coeficiente de arrasto parasita da Empenagem Vertical
$C_{D_{0_{LG}}}$ Coeficiente de arrasto parasita do Trem de Pouso
$C_{D_{0_N}}$ Coeficiente de arrasto parasita da Nacele
$C_{D_{0_S}}$ Coeficiente de arrasto parasita do Strut
$C_{D_{0_{HLD}}}$ Coeficiente de arrasto parasita de Dispositivos Hiper Sustentadores
2.3.1 Coeficiente de arrasto parasita da fuselagem ($C_{D_{0_f}}$ )
O coeficiente de arrasto parasita da Fuselagem é dado pela seguinte equação :
\[\begin{equation} C_{D_{0_f}}=C_{f_f} f_{LD} f_M\frac{S_{wet_f}}{S} \end{equation}\]- $C_{f_f}$ é o coeficiente de fricção de fusleagem, que é definido pelo coeficiente de fricção da relação de Prandtl
Para determinar o coeficiente de fricção para fuselagem calculamos antes o número de Reynolds. O admimensional $Re$ é dado pela seguinte relação : \(\begin{equation} Re=\frac{\rho V L}{\mu } \end{equation}\)
Onde :
$\rho$: Densidade do ar Local
$V$: Velocidade verdadeira da aeronave
$\mu$: Viscosidade dinâmica do ar
$L$: Comprimento da fuselagem
Para $Re$ $<$ 200.000 adotaremos o fluxo como laminar e para $Re$$>$ 2.000.000 adotaremos o fluxo como turbulento
Considerando que a aeronave voa em maior parte da missão no seu nível de voo de cruzeiro, iremos estimar nosso número de Reynolds com base no FL250($\rho_{FL250}=0,5489$), uma viscosidade dinâmica do ar($\mu=2,8050\times10^{-5}$), velocidade de cruzeiro de 400 knot e um comprimento de fuselagem de $27,93 m$ :
\[\begin{equation*} Re=\frac{0,5489\cdot(400\cdot0,5144)\cdot 27,93}{1,53826\times10^{-5}}= 2,05\times 10^{8} \end{equation*}\]Ou seja, temos um Reynolds turbulento, portanto usaremos a equação(10) para determinar o Coeficiente de fricção da fuselagem baseado na relação de Prandtl tão logo ($C_{f_f}$) será:
\[\begin{equation*} C_{f_f}= 0,00192 \end{equation*}\]- ${f_{LD}}$ é um coeficiente que relaciona o comprimento da fuselagem com o seu diâmetro, que é definido como :
Onde:
$L$ é o comprimento da fuselagem
$D$ é o diâmetro máximo da fuslagem
Esses dados são facilmente encontrados na lista de dimensões gerais do EMB-145. Substituindo os valores temos:
\[\begin{equation*} {f_{LD}} = 1,06212 \end{equation*}\]- ${f_M}$ é o coeficiente que relaciona com o Número de Mach, definido como : \(\begin{equation} {f_M}= 1-0,08M^{1.45} \end{equation}\)
De acordo com os dados de desempenho da aeronave sabemos que a mesma voa em M = 0,78 substituindo M na equação (14) temos:
\[\begin{equation*} {f_M}=0,94420 \end{equation*}\]$\displaystyle{\frac{S_{wet_f}}{S}}$ É a relação entre área molhada total da fuselagem e área de referência da Asa.
A área molhada, é a área que é exposta ao escoamento de ar duarante o voo. Para determiná-lo pode-ser usar relações empíricas de aeronaves já produzidas através de tabelas ou pode-se usar softwares CAD para estimar com mais precisão a área molhada de cada componente da aeronave. Para nosso trabalho usamos um modelo CAD do embraer 145 disponível para download, conforme imagem e tabela abaixo:
EMB-145 no Solidworks
Tabela 2: Área molhada por componente
| Componente | Nomenclatura | Área ($m^2$) |
|---|---|---|
| Fuselagem | $S_{wet_f}$ | 190,00 |
| Asa | $S_{wet_w}$ | 87,00 |
| Empenagem Vertical | $S_{wet_{vt}}$ | 24,28 |
| Empenagem Horizontal | $S_{wet_{ht}}$ | 24,72 |
| Nacele | $S_{wet_n}$ | 18,00 |
| Pylone | $S_{wet_{pl}}$ | 6,70 |
| Total | $S_{wet}$ | 350,00 |
Sabendo que a área de referência da asa é de $51,18 m^2$ temos todos os valores necessários para determinar o coeficiente de arrasto parasita da fuselagem, substituindo os valores encontrados na equação (9) temos:
\[\begin{align*} C_{D_{0_f}}&=0,00192\cdot1,06212\cdot0,94420\cdot\left(\frac{190}{51,18}\right)\\ C_{D_{0_f}}&=0,007148 \end{align*}\]2.3.2 Coeficiente de arrasto Parasita da Asa ($C_{D_{0_w}}$)
Seguindo a metodologia apresentada em 1 o equacionamento para o cálculo do coeficiente de arrasto parasita da asa se dá da seguinte maneira :
\[\begin{equation} C_{D_{0_w}} = C_{f_w} \cdot f_{tc_w} \cdot f_M \cdot \frac{S_{\text{wet}_w}}{S} \left( \frac{C_{d_{\min_w}}}{0,004} \right)^{0,4} \end{equation}\]Para o cálculo de $C_{f_w}$ usamos a relação de Prandtl usada para o cálculo da fuseleagem porém o comprimento característico utilizado no cáclulo do número de Reynolds agora, é a corda média aerodinâmica da asa($cma$), cujo valor é de $2,86m$, tão logo teremos um Número de Reynolds para asa de :
\[\begin{equation*} Re_{w}\overset{\sim}{=} 2,1\times 10^{7}. \end{equation*}\]Conforme foi visto para o Reynolds Turbulento usamos a equação (10) que nos dá um $C_{f_w}$:
\[\begin{equation*} C_{f_w} = 0,00267 \end{equation*}\]${f_M}$ é o coeficiente que relaciona com o Número de Mach, definido como :
\[\begin{equation*} {f_M}= 1-0,08M^{1,45} \end{equation*}\]Para a asa o valor de ${f_M}$ será o mesmo que o encontrado para fuselagem:
${f_M}=0,94420 $
$f_{tc_{w}}$ É o parâmetro que relaciona razão de espessura máxima da asa. Seu equacionamento é dado da seguinte maneira :
\[\begin{equation} f_{tc_{w}} = 1 + 2.7\left(\frac{t}{c}\right)_{\text{max}} + 100\left(\frac{t}{c}\right)_{\text{max}}^{4} \end{equation}\]O perfil aerodinâmico usado no EMB-145LR é de informação confidencial da EMBRAER porém sabe-se que trata-se de um aerofólio super crítico, desenvolvido pela própria fabricante. Nesse caso para determinar as características do perfil tivemos que usar os desenhos CAD disponíveis em 4 para estimar o seu formato e conseguir determinar a sua espessura relativa máxima.
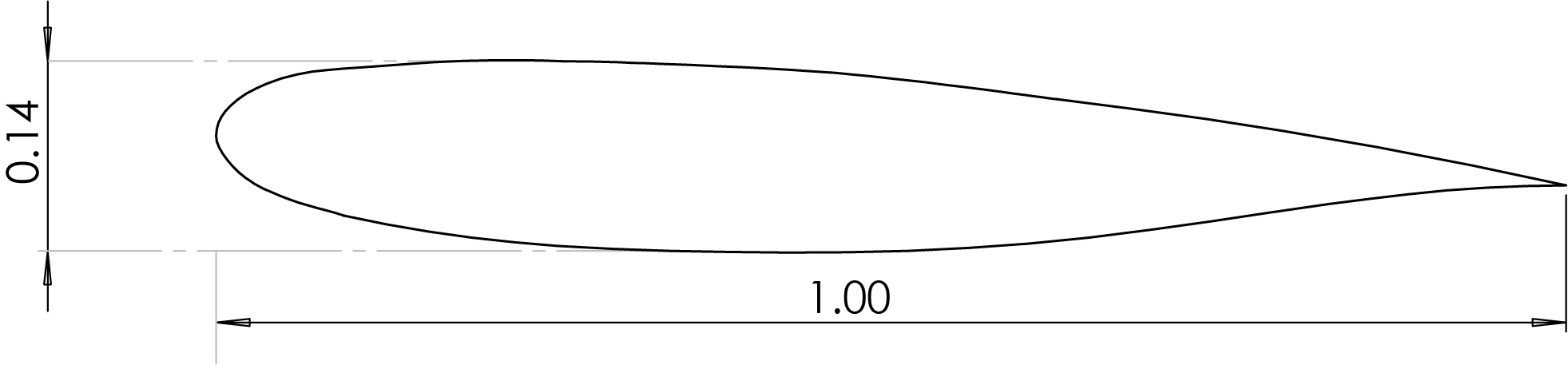Vista lateral do Aerofólio supercrítico usado no EMB-145LR
Conforme a imagem acima, percebemos que o perfil possui espessura máxima relativa a corda de 14\%, substituindo esse valor na equação (16) temos :
\[\begin{align*} f_{tc_w} = 1,4164 \end{align*}\]Para a relação entre a área molhada da asa e sua área de referência, consultando a Tabela 2 e na da lista de dimensões da aeronave encontramos :
\[\begin{equation*} \frac{S_{wet_w}}{S}=1,69988 \end{equation*}\]Para determinar o $C_{d_{\min_w}}$ do aerofólio usamos como referência o perfil encontrado nos desenhos CAD e plotamos um novo aerofólio no software XFLR-5. Após criar o novo aerofólio dentro do software, realizamos uma análise para $Re_{w}\overset{\sim}{=} 2,1\times 10^{7}$ e variamos o ângulo de ataque do perfil para obter a polar de arrasto e determinar o $C_{d_{min_w}}$ . A imagem abaixo refere-se ao gráfico da polar de arrasto obtida pelo XFLR-5 :
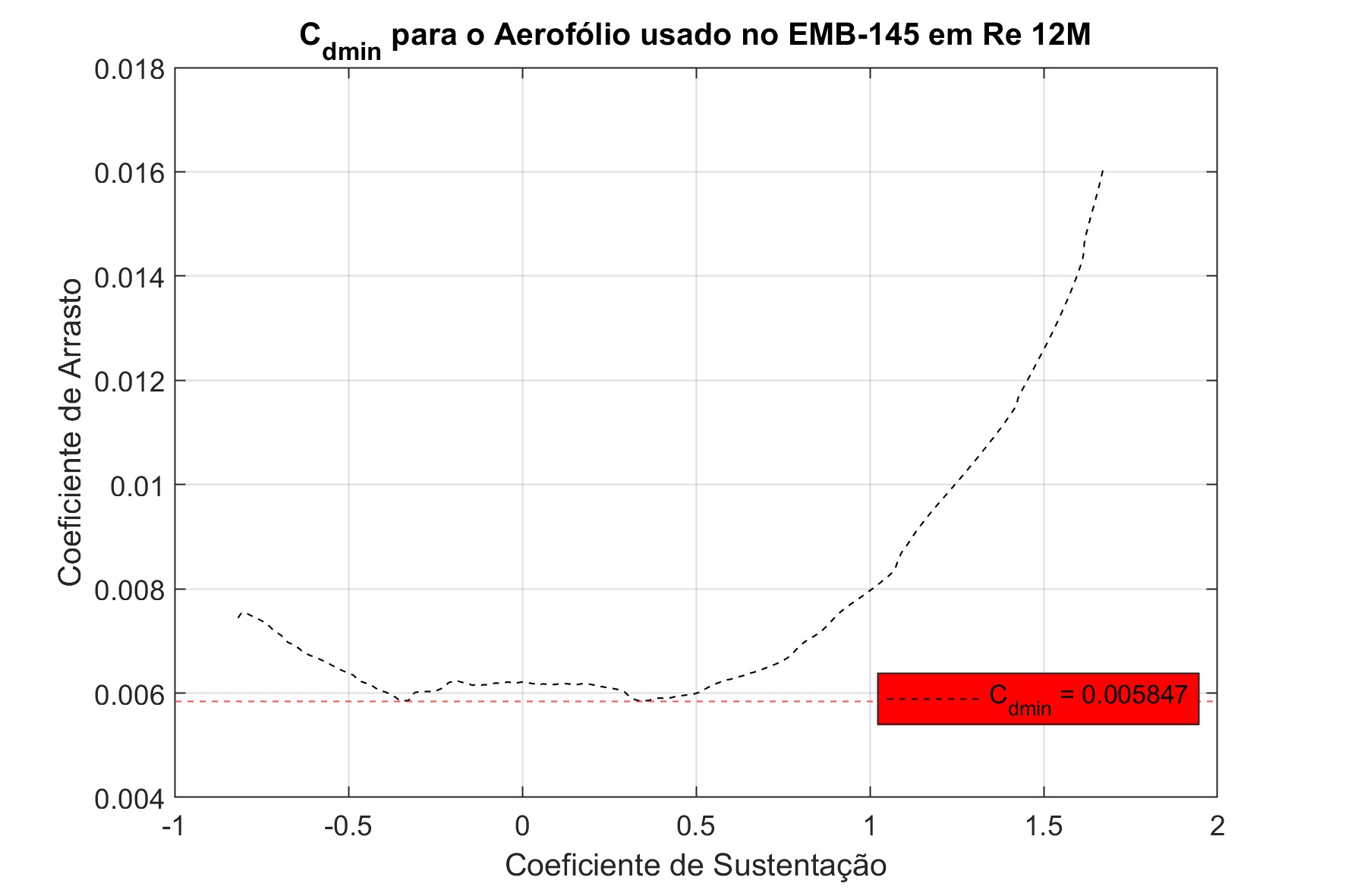Polar de Arrasto do aerofólio da raiz do emb-145LR
Determinados todos os coeficientes necessários, podemos calcular o arrasto parastita da asa $C_{D_{0_w}}$ substituindo os valores calculados acima :\
\[\begin{aligned} C_{D_{0_w}} &= 0,00267 \cdot 1,4164 \cdot 0,94420 \cdot 1,69988 \cdot \left(\frac{0,005847}{0,004}\right)^{0,4} \\ C_{D_{0_w}} &= 0,00707 \end{aligned}\]2.3.3 Coeficiente de arrasto parasita da EH e EV
As empenagens horizontal e vertical podem ser consideradas asas menores, por isso a metodologia para o cálculo do coeficiente de arrasto parasita irá seguir o mesmo procedimento adotado para as asas.
Para determinação dos coeficientes de fricção para EH e EV precisamos saber qual o Número de Reynolds adotado para essas superfícies, sabendo que:
\[\begin{aligned} cma_{eh} &= 1,53\text{m} \\ cma_{ev} &= 2,63\text{m} \end{aligned}\]Tão logo considerando as mesmas condições de voo adotadas para o cálculo de Reynolds da asa e substituindo os valores na equação (12) temos:
\[\begin{aligned} Re_{eh} &= 1,12 \times 10^{7} \\ Re_{ev} &= 1,92 \times 10^{7} \end{aligned}\]Determinado o Número de Reynolds e sabendo que os valores encontrados são Reynolds turbulento, calculamos os coeficientes de fricção:
\[\begin{aligned} C_{f_{eh}} &= 0,00294 \\ C_{f_{ev}} &= 0,00270 \end{aligned}\]Para a EH e EV o fator de razão de espessura máxima relativa adotado será de 12% referente ao NACA0012 desse modo $f_{tc_{eh}}$ e $f_{tc_{ev}}$ serão os mesmos, a metodologia de cálculo é a mesma que fora usada para a asa, tão logo:
\[f_{tc_{eh}} = f_{tc_{ev}} = 1,3447\]O coeficiente que relaciona com o Número de Mach é $f_M$, considerando $M0,78$ temos:
\[\begin{aligned} f_M &= 1 - 0,08M^{1,45} \\ f_M &= 0,94420 \end{aligned}\]A relação entre as áreas molhadas é encontrada na Tabela de áreas molhadas por componente:
\[\begin{aligned} \frac{S_{\text{wet}_{eh}}}{S} &= \frac{24,72}{51,18} = 0,48300 \\ \frac{S_{\text{wet}_{ev}}}{S} &= \frac{24,28}{51,18} = 0,47440 \end{aligned}\]Para determinar o $C_{d_{\min_{eh}}}$ e o $C_{d_{\min_{ev}}}$ adotaremos que o perfil aerodinâmico usado nessas empenagens é o NACA0012 comumente adotado para empenagens.
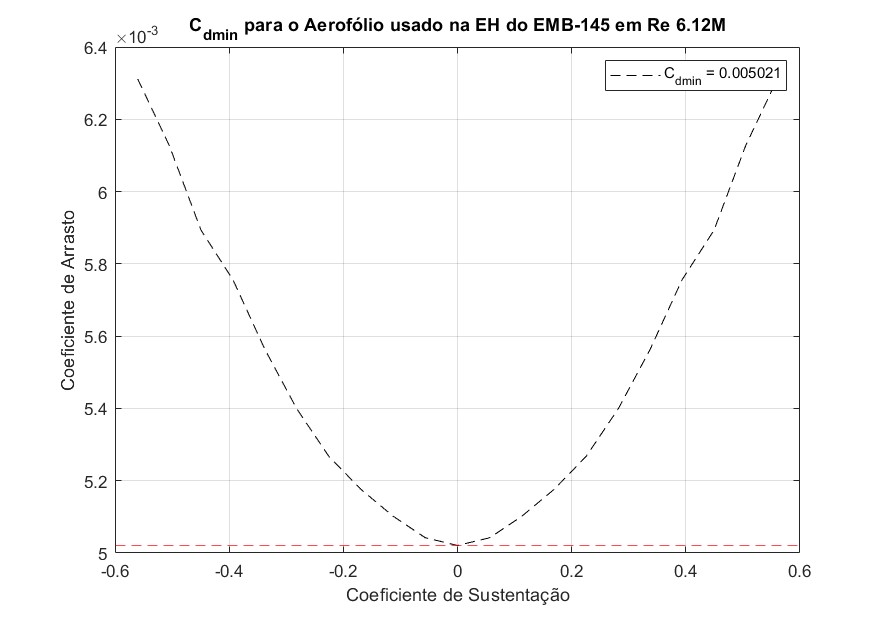($C_{d_{\min_{eh}}}$) para o aerofólio usado na empenagem horizontal
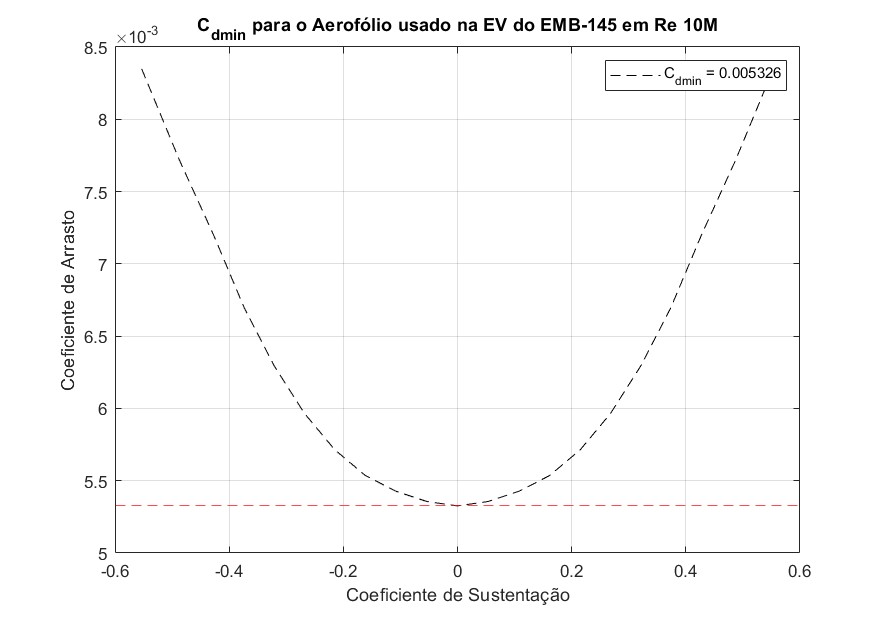($C_{d_{\min_{ev}}}$) para o aerofólio usado na empenagem vertical
Com todos os coeficientes calculados podemos obter o arrasto parasita da EH e EV:
\[\begin{aligned} C_{D_{0_{eh}}} &= 0,00294 \cdot 1,3447 \cdot 0,94420 \cdot 0,48300 \left(\frac{0,005021}{0,004}\right)^{0,4} = 0,00197 \\ C_{D_{0_{ev}}} &= 0,00270 \cdot 1,3447 \cdot 0,94420 \cdot 0,47440 \left(\frac{0,005326}{0,004}\right)^{0,4} = 0,00159 \end{aligned}\]2.3.4 Coeficiente de Arrasto Parasita do Trem de Pouso ($C_{D_{0_{LG}}}$)
Para o equacionamento do arrasto parasita do trem de pouso usaremos a seguinte equação:
\[C_{D_{0_{LG}}} = \sum_{i=1}^{n} C_{d_{lg}} \left( \frac{S_{lg_i}}{S} \right)\]Onde:
- $C_{d_{lg}}$ é o coeficiente de arrasto para trem de pouso
- $S_{lg_i}$ é a área frontal de cada roda
- $S$ é a área de referência da asa
O coeficiente de arrasto parasita para o trem de pouso ($C_{d_{lg}}$) varia entre $0,15$ para rodas com carenagens e $0,30$ para rodas sem carenagens. Para o EMB-145LR adotaremos rodas sem carenagens. Para determinar a área frontal das rodas utilizamos desenhos técnicos para estimar suas dimensões.
Portanto o $C_{d_{lg}}$ para o trem de pouso principal será:
\[\begin{aligned} C_{D_{0_{LG}}} &= \sum_{i=1}^{4} 0,30 \left( \frac{0,165}{51,18} \right) \\ C_{D_{0_{LG}}} &= 4 \cdot (0,000967) \\ C_{D_{0_{LG}}} &= 0,003868 \end{aligned}\]Para o trem de pouso dianteiro teremos:
\[\begin{aligned} C_{D_{0_{LG}}} &= \sum_{i=1}^{2} 0,30 \left( \frac{0,0936}{51,18} \right) \\ C_{D_{0_{LG}}} &= 2 \cdot (0,000548) \\ C_{D_{0_{LG}}} &= 0,001097 \end{aligned}\]Somando os coeficientes para trem de pouso principal e trem de pouso dianteiro teremos o $C_{D_{0_{LG}}}$ como um todo:
\[\begin{aligned} C_{D_{0_{LG}}} &= (0,003868) + (0,001097) \\ C_{D_{0_{LG}}} &= 0,004965 \end{aligned}\]2.3.5 Coeficiente de Arrasto Parasita de Nacele ($C_{D_{0_N}}$)
Para o cálculo do coeficiente de arrasto parasita da nacele adotaremos o mesmo princípio usado para o cálculo da fuselagem. Fazendo o procedimento de cálculo, temos:
\[C_{D_{0_N}} = 0,0005\]No entanto a aeronave possui dois motores carenados, tão logo devemos multiplicar o valor por $2$ de tal maneira que encontramos:
\[C_{D_{0_N}} = 0,0011\]2.3.6 Coeficiente de Arrasto devido ao Flap ($C_{D_{0_{flap}}}$)
A equação para determinar o arrasto parasita dos flaps é:
\[C_{D_{0_{flap}}} = \left( \frac{C_f}{C} \right) A \cdot (\delta_f)^{B}\]Onde:
- $C_f$ é a corda extendida do Flap
- $C$ é a corda da Asa
- $\delta_f$ é a deflexão dos flaps em graus
- $A$ e $B$ são parâmetros dados pela tabela abaixo:
Tabela 3- Valores A e B para diferentes tipos de Flaps
| Tipo de Flap | A | B |
|---|---|---|
| Split Flap | 0,0014 | 1,5 |
| Plain Flap | 0,0016 | 1,5 |
| Single-Slotted Flap | 0,00018 | 2,0 |
| Double-Slotted Flap | 0,001 | 1,0 |
| Fower | 0,00015 | 1,5 |
O EMB-145LR utiliza flaps do tipo Fower, as deflexões dos flaps variam para decolagem e pouso. Para decolagem utiliza-se um pente ou três pentes de flap ($9^\circ$ ou $22^\circ$) para o pouso utiliza-se full flap ($45^\circ$). Essa aeronave possui dois flaps em cada asa, um flap interno mais próximo a fuselagem e outro mais externo próximo aos ailerons e da ponta da asa.
Cálculo do Arrasto Parasita do Flap na decolagem ($22^\circ$)
Flap Interno:
\[\begin{aligned} C_{D_{0_{flap}}} &= \left( \frac{0,836}{3,052} \right) 0,00015 \cdot (22)^{1,5} \\ C_{D_{0_{flap}}} &= 0,0042 \end{aligned}\]Flap Externo:
\[\begin{aligned} C_{D_{0_{flap}}} &= \left( \frac{0,651}{1,862} \right) 0,00015 \cdot (22)^{1,5} \\ C_{D_{0_{flap}}} &= 0,0054 \end{aligned}\]Cálculo do Arrasto Parasita do Flap no pouso ($45^\circ$)
Flap Interno:
\[\begin{aligned} C_{D_{0_{flap}}} &= \left( \frac{0,836}{3,052} \right) 0,00015 \cdot (45)^{1,5} \\ C_{D_{0_{flap}}} &= 0,0124 \end{aligned}\]Flap Externo:
\[\begin{aligned} C_{D_{0_{flap}}} &= \left( \frac{0,651}{1,862} \right) 0,00015 \cdot (45)^{1,5} \\ C_{D_{0_{flap}}} &= 0,0158 \end{aligned}\]Somando os valores encontrados para flaps internos e externos temos:
Arrasto Parasita dos Flaps na decolagem ($22^\circ$):
\[C_{D_{0_{flap-TO}}} = 0,0096\]Arrasto Parasita dos Flaps no Pouso ($45^\circ$):
\[C_{D_{0_{flap-L}}} = 0,0282\]3. Arrasto Parasita na Condição Limpa ($C_{D_{0_{clean}}}$)
Para essa condição de arrasto consideramos o arrasto parasita de todos os componentes, excluídos o trem de pouso e os flaps, dessa forma temos:
\[C_{D_{0_{clean}}} = C_{D_{0_f}} + C_{D_{0_w}} + C_{D_{0_{ht}}} + C_{D_{0_{vt}}} + C_{D_{0_N}}\]Substituindo os valores calculados na seção anterior teremos:
\[\begin{aligned} C_{D_{0_{clean}}} &= 0,007148 + 0,00707 + 0,00197 + 0,00159 + 0,0011 \\ C_{D_{0_{clean}}} &= 0,01887 \end{aligned}\]4. Polar de Arrasto na Condição Limpa ($C_{D_{clean}}$)
Para o cálculo da polar de arrasto na condição limpa, consideramos a aeronave voando em nível de voo de cruzeiro, o equacionamento para essa polar é:
\[C_{D_{clean}} = C_{D_{0_{clean}}} + K(C_{L_c})^2\]Onde:
- $K$ é o coeficiente de arrasto induzido
- $C_{D_{0_{clean}}}$ é o coeficiente de arrasto parasita na condição limpa
- $C_{L_c}$ é o Coeficiente de Sustentação para o voo em cruzeiro
Para determinar o coeficiente de sustentação para o voo em cruzeiro utilizamos a seguinte equação:
\[\begin{aligned} C_{L_c} &= \sqrt{\frac{C_{D_0}}{3K}} \\ C_{L_c} &= \sqrt{\frac{0,01887}{3(0,0485)}} \\ C_{L_c} &= 0,36 \end{aligned}\]Substituindo os valores na equação teremos:
\[\begin{aligned} C_{D_{clean}} &= 0,01887 + 0,0485(0,36)^2 \\ C_{D_{clean}} &= 0,0251 \end{aligned}\]5. Arrasto Parasita na Condição de Decolagem ($C_{D_{0_{TO}}}$)
Nessa condição consideramos o arrasto parasita de todos os componentes acrescidos do arrasto parasita do flap para essa condição ($22^\circ$) e o arrasto parasita do trem de pouso.
\[\begin{aligned} C_{D_{0_{TO}}} &= C_{D_{0_{clean}}} + C_{D_{0_{flap-TO}}} + C_{D_{0_{LG}}} \\ C_{D_{0_{TO}}} &= 0,01887 + 0,0054 + 0,004965 \\ C_{D_{0_{TO}}} &= 0,0292 \end{aligned}\]6. Polar de Arrasto na Condição de Decolagem ($C_{D_{TO}}$)
Para determinar a polar de arrasto para decolagem usamos a seguinte equação:
\[C_{D_{TO}} = C_{D_{0_{TO}}} + K(C_{L_{TO}})^2\]Para determinação do coeficiente de sustentação de decolagem usamos a seguinte equação:
\[C_{L_{TO}} = 0,9 \frac{2mg}{\rho S(V_{LO})^2}\]Onde:
\[V_{LO} = K_{LO} V_S\]Sendo que:
- $K_{LO}$ varia entre 1,1-1,3
- Para determinar a velocidade de stall precisamos encontrar o valor de $C_{L_{max}}$ dessa aeronave
Tabela 4 -Coeficiente de Sustentação Máximo por Categoria de Aeronaves
| Tipo de Aeronave | $C_{L_{max}}$ | $V_{stall}$ (Knot) |
|---|---|---|
| Asa Delta | 2.5-3.5 | 10-15 |
| Planadores | 1.8-2.5 | 12-25 |
| Ultraleve | 1.8-2.4 | 20-30 |
| Aeronaves Leves Esportivas | 1.6-2.2 | 30-45 |
| Aviação Geral Leve | 1.6-2.2 | 40-61 |
| Agrícolas | 1.5-2.0 | 45-61 |
| Amadoras | 1.2-1.8 | 40-70 |
| Jatos Executivos | 1.6-2.6 | 70-120 |
| Transporte a Jato | 2.2-3.2 | 95-130 |
| Caças Supersônicos | 1.8-3.2 | 100-120 |
6.1 Determinando a Velocidade de Stall da Aeronave ($V_{stall}$)
Com base na tabela acima, iremos adotar um $C_{L_{max}}$ de 2,2 para o EMB-145LR. Considerando o nível do mar $\rho = 1,225 \text{ kg/m}^3$, um MTOW de 22.000 kg, área de asa ($S$) de 51,18 m². Dessa forma a velocidade de stall será:
\[\begin{aligned} V_{stall} &= \sqrt{\frac{2mg}{\rho S C_{L_{max}}}} \\ V_{stall} &= \sqrt{\frac{2(22.000 \cdot 9,81)}{1,225 \cdot 51,18 \cdot 2,2}} \\ V_{stall} &= 55,94 \text{ m/s} = 108,75 \text{ knot} \end{aligned}\]Com a velocidade de stall determinada podemos calcular o coeficiente de sustentação para decolagem, adotando um $K_{LO}$ de 1,1:
\[\begin{aligned} C_{L_{TO}} &= 0,9 \frac{2(22.000 \cdot 9,81)}{1,225 \cdot 51,18 (1,1 \cdot 55,94)^2} \\ C_{L_{TO}} &= 1,636 \end{aligned}\]Encontrado o valor para o coeficiente de sustentação de decolagem podemos determinar finalmente a polar de arrasto para condição de decolagem:
\[\begin{aligned} C_{D_{TO}} &= 0,0292 + 0,0485(1,636)^2 \\ C_{D_{TO}} &= 0,159 \end{aligned}\]6.2 Arrasto Parasita na Condição de Pouso ($C_{D_{0_L}}$)
O equacionamento para essa condição se dá da seguinte maneira:
\[\begin{aligned} C_{D_{0_L}} &= C_{D_{0_{clean}}} + C_{D_{0_{flap-L}}} + C_{D_{0_{LG}}} \\ C_{D_{0_L}} &= 0,01887 + 0,0282 + 0,00496 \\ C_{D_{0_L}} &= 0,0520 \end{aligned}\]7. Polar de Arrasto na Condição de Pouso ($C_{D_L}$)
Para essa condição seguimos o equacionamento abaixo:
\[C_{D_L} = C_{D_{0_L}} + K(C_{L_L})^2\]Seguindo a mesma metodologia para a decolagem, adotamos um $K_L$ de 1,3 e multiplicamos esse fator pela velocidade de stall para obtermos a velocidade de pouso da aeronave. Encontrada a velocidade de pouso substituímos na equação abaixo:
\[\begin{aligned} C_{L_L} &= \frac{2(22.000 \cdot 9,81)}{1,225 \cdot 51,18 (1,3 \cdot 55,94)^2} \\ C_{L_L} &= 1,301 \end{aligned}\]Substituindo os valores na equação temos:
\[\begin{aligned} C_{D_L} &= 0,0520 + 0,0485(1,301)^2 \\ C_{D_L} &= 0,134 \end{aligned}\]7.1 Arrasto Parasita Completo
A tabela abaixo foi montada no intuito de reunir todos os arrastos parasitas calculados acima, ou seja para as condições: limpa, decolagem e pouso.
Tabela 5- Arrasto parasita para as condições
| Configuração | $C_{D_0}$ |
|---|---|
| Limpa | 0,0188 |
| Decolagem | 0,0292 |
| Pouso | 0,0520 |
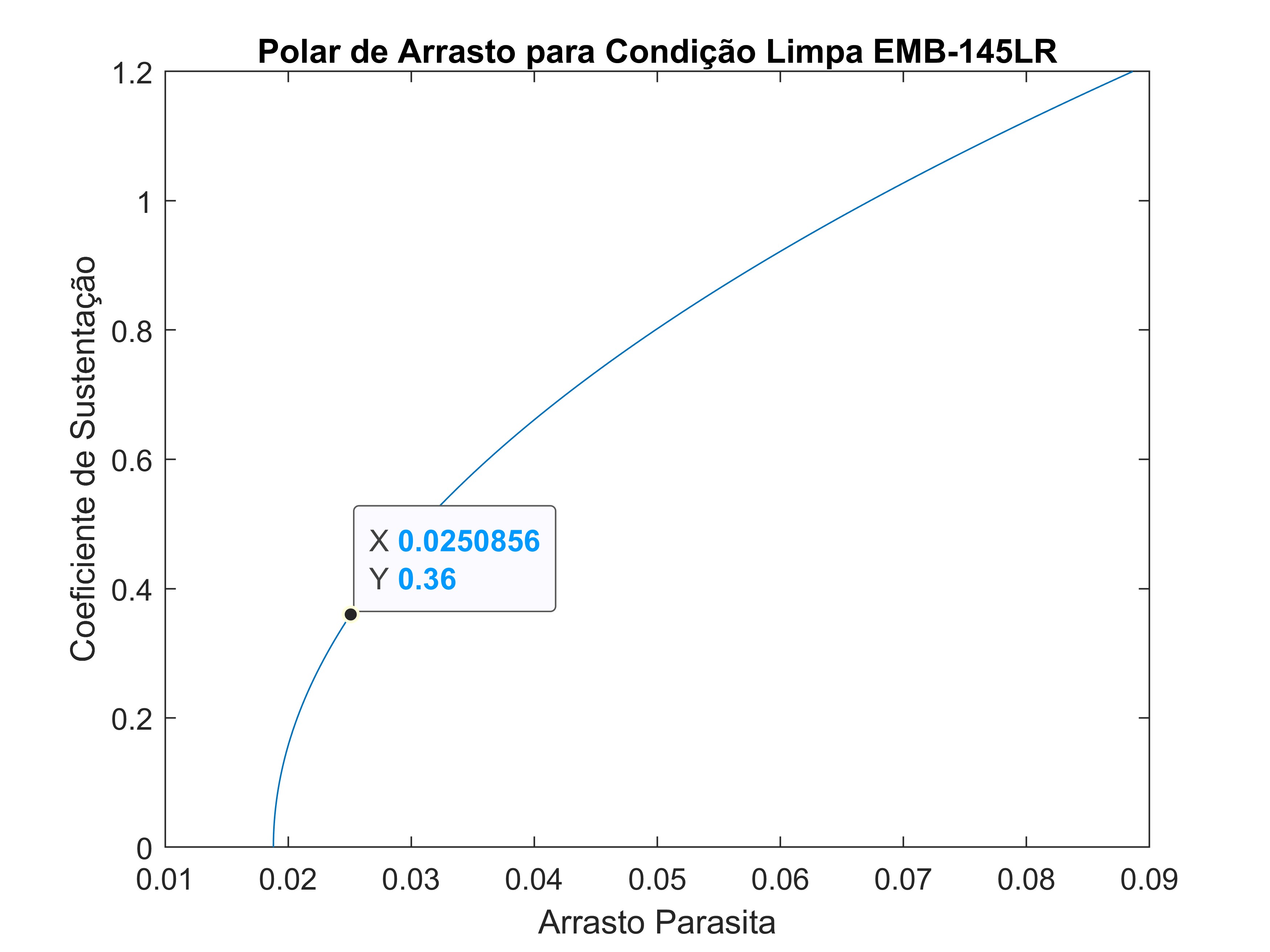Polar de arrasto para condição Limpa
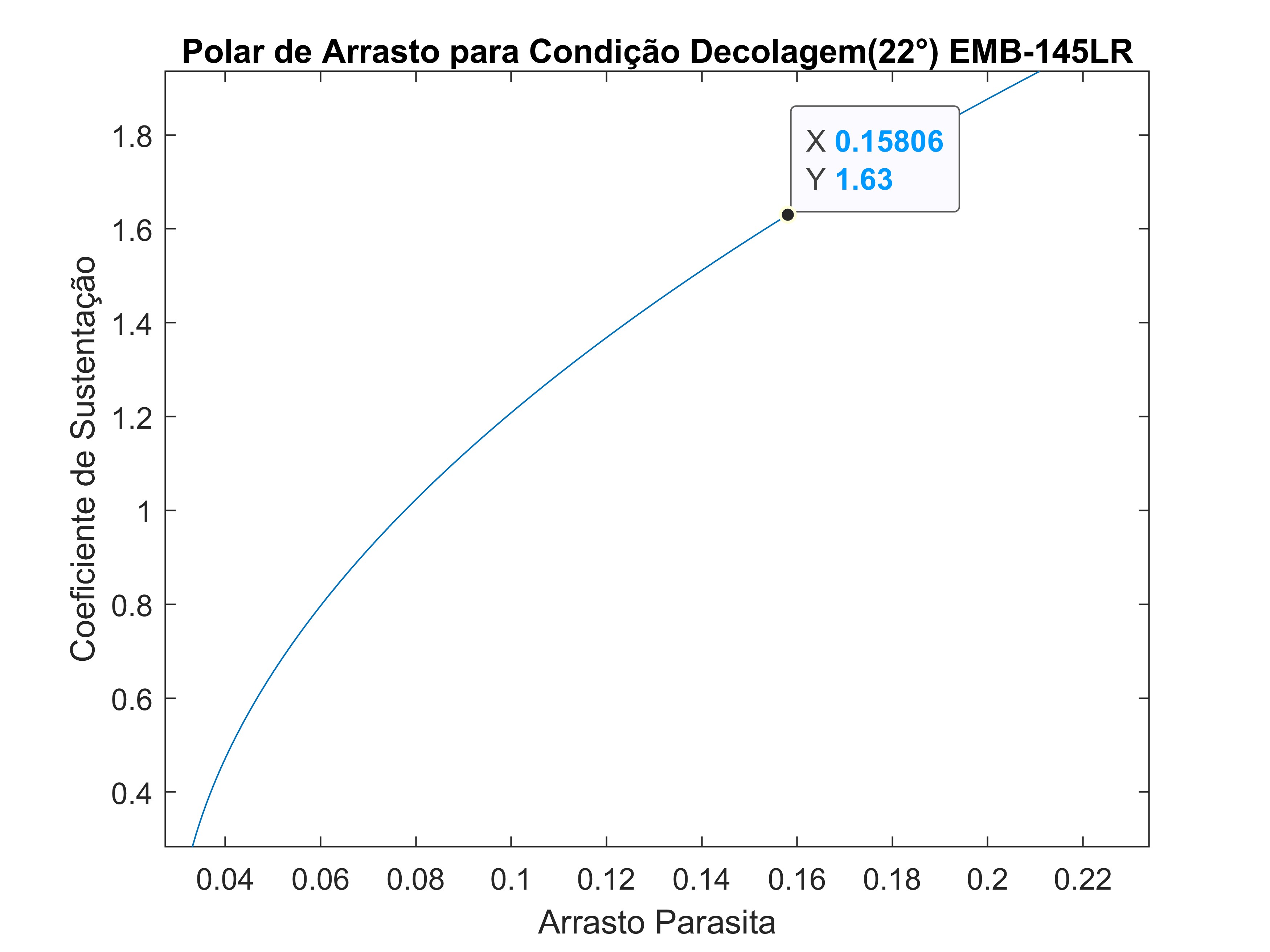Polar de arrasto para condição de Decolagem
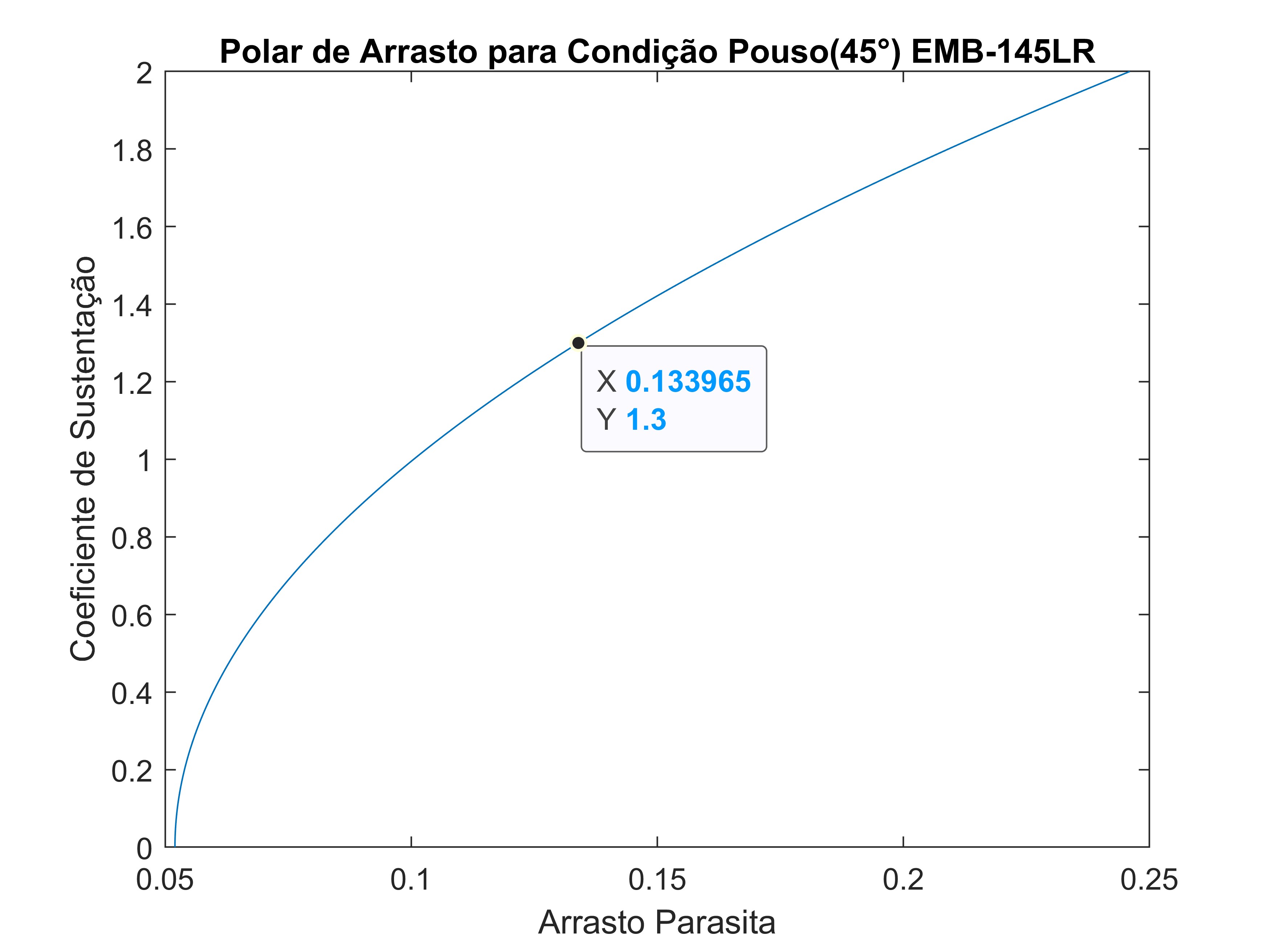Polar de arrasto para condição de Pouso
8. Velocidade Máxima ($V_{max}$)
Dentro das análises de desempenho de uma aeronave, a velocidade máxima alcançada é um critério bastante relevante para que a aeronave possa desenvolver um bom desempenho em voo de cruzeiro. Aeronaves de transportes a jato voando mais rápido reduzem o tempo entre as viagens, podendo efetuar mais voos para um mesmo dia, sendo mais lucrativo para o operador e mais comodidade para o passageiro que chega a seu destino mais rápido.
Para caças, a velocidade máxima impacta diretamente no campo de batalha e em sua furtividade. A velocidade máxima sustentada em nível de voo é alcançada quando o motor atinge seu empuxo máximo. Visando manter a integridade física dos motores e da estrutura da aeronave, dificilmente uma aeronave voará em sua velocidade máxima.
Para determinar diretamente a velocidade máxima em FL250 para o EMB-145LR usamos o equacionamento a seguir:
\[V_{\max} = \left\{ \frac{ \left[ \left( \frac{T_A}{W} \right)_{\max} \cdot \frac{W}{S} \right] + \frac{W}{S} \sqrt{ \left( \frac{T_A}{W} \right)_{\max}^2 - 4 C_{D_0} K } }{ \rho_{FL} C_{D_0} } \right\}^{1/2}\]Onde:
- $W$ é o peso da aeronave (neste caso MTOW)
- $S$ é a área de referência da Asa
- $C_{D_0}$ é o arrasto parasita da aeronave na condição limpa
- $K$ é o coeficiente de arrasto induzido da aeronave
- $\rho_{FL}$ é a densidade do ar para o nível de voo
- $\left( T_A \right)_{\max}$ é dado por:
Fazendo as devidas substituições e cálculo, encontramos:
\[\begin{aligned} V_{\max} &= 264,84 \text{ m/s} \\ V_{\max} &= 0,85 \text{ M} \end{aligned}\]9. Máximo Alcance ($R_{max}$)
Para determinar o alcance máximo da aeronave, devemos usar as equações de Breguet. Porém existem três formas para o voo em cruzeiro. São elas:
- Diminuindo a velocidade de voo (voo de altitude constante, coeficiente de sustentação constante)
- Aumentando a altitude (voo de velocidade constante, coeficiente de sustentação constante)
- Diminuindo ângulo de ataque (voo de altitude constante, velocidade do ar constante)
Esses três programas de voo de cruzeiro nos fornecem diferentes alcances, cada um com suas características, conforme visto acima. No entanto, voos comerciais são separados verticalmente por altitudes fixas e delimitadas ao longo do voo. Esse monitoramento é realizado por um centro de controle de tráfego aéreo. Para tal, devemos considerar o programa número 3, onde a altitude não varia durante o voo de cruzeiro e a velocidade permanece constante.
9.1 Alcance Máximo utilizando o programa de cruzeiro 3 ($R_{3_{max}}$)
Seguindo as equações de Breguet para cada programa teremos para essa condição a seguinte equação:
\[R_3 = \left[ \frac{V_{md}}{TSFC} E_{\max} \right] 2 u_i \left\{ \tan^{-1} \left[ \frac{1}{u_i^2} \right] - \tan^{-1} \left[ \frac{1}{\omega u_i^2} \right] \right\}\]Onde:
- $E_{\max} = \left( \frac{C_L}{C_D} \right)_{\max}$ (Eficiência Aerodinâmica Máxima)
- $V_{md} = \sqrt{ \frac{2W_i}{\rho S C_{L_{md}}} }$ (Velocidade de Mínimo Arrasto)
- $TSFC = 0,0001 \text{ 1/s}$ (Consumo Específico de Combustível por segundo para o motor AE3001)
- $u = \frac{V_{cruise}}{V_{md}}$ (Velocidade Relativa)
- $\omega = \frac{\omega_i}{\omega_f}$ (Relação entre pesos da aeronave)
- $\omega_i =$ Peso de Decolagem da aeronave (TOW)
- $\omega_f =$ Peso Final da aeronave (LW)
Considerando que a aeronave voa em FL370, possui um peso de decolagem de 190.108,00 [N] e um peso de pouso de 175.599,00 [N] voa com 50 passageiros + carga máxima, encontramos um alcance máximo de:
\[\begin{aligned} R_3 &= 2.845,97 \text{ [km]} \\ R_3 &= 1.536 \text{ [nm]} \end{aligned}\]10. Máxima Autonomia utilizando o programa de cruzeiro 3 ($E_{3_{max}}$)
Seguindo a mesma metodologia para o cálculo do alcance máximo, para encontrar a autonomia máxima, isso é, o tempo máximo no qual a aeronave pode ficar voando, teremos a seguinte equação:
\[E_{3_{max}} = \left[ \frac{E_{\max}}{TSFC} \right] 2 \left\{ \tan^{-1} \left[ \frac{1}{u_i^2} \right] - \tan^{-1} \left[ \frac{1}{\omega u_i^2} \right] \right\}\]Fazendo as devidas substituições teremos:
\[E_{3_{max}} = 3,8187 \text{ [horas]}\]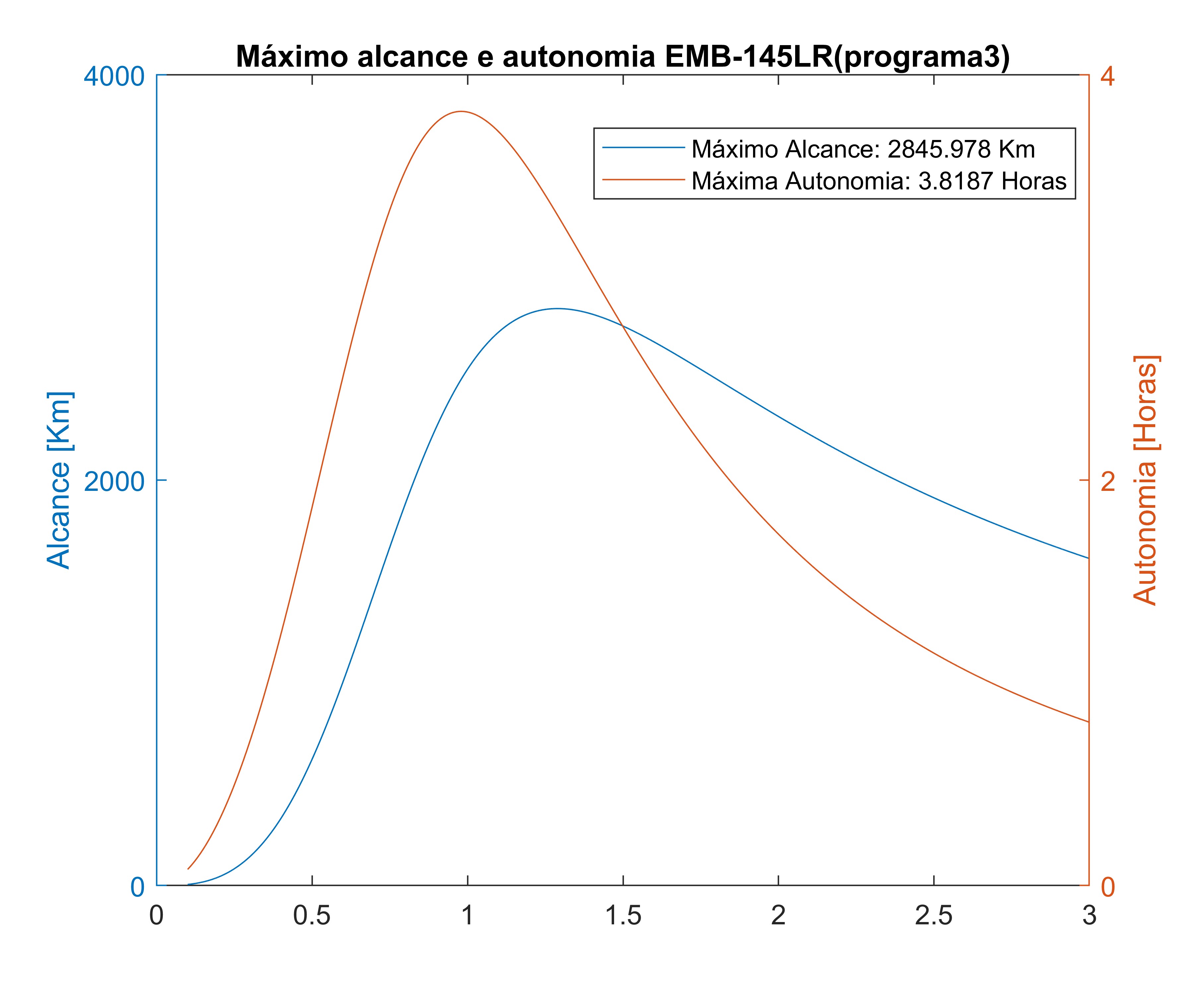
Máxima Autonomia e Alcance para EMB-145LR
11. Razão de Subida Máxima ($ROC_{max}$) e Teto de Serviço
A razão de subida máxima ($ROC_{max}$) é um dos parâmetros cruciais no desempenho de uma aeronave. Ela determina a capacidade da aeronave de subir rapidamente e superar obstáculos como montanhas e formações meteorológicas perigosas. Em essência, o $ROC_{max}$ depende da máxima diferença entre as curvas de máxima potência disponível e potência requerida, além do peso da aeronave.
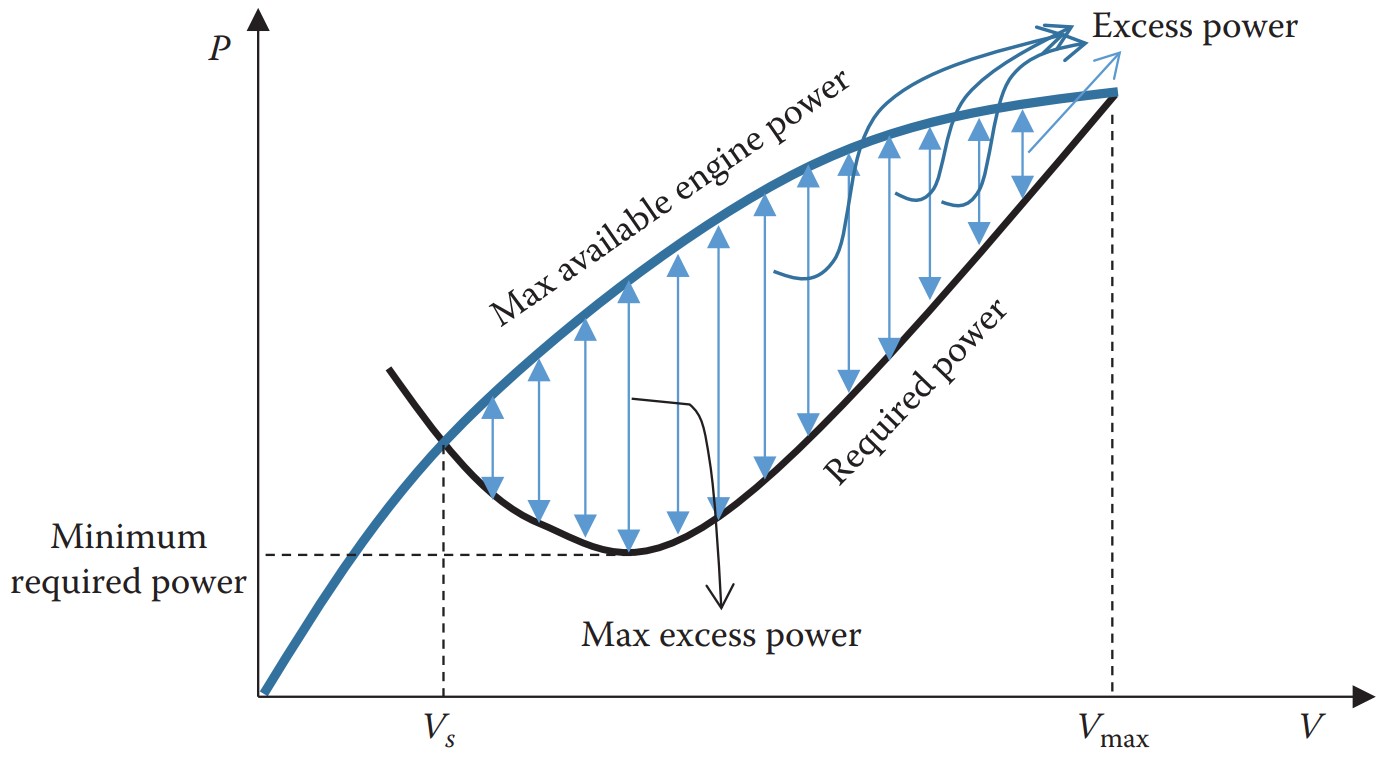Curva de Potência Requerida vs Potência disponível para uma aeronave genérica
Fazendo repetidamente o cálculo de $ROC_{max}$ para cada altitude e obtendo o excesso de potência naquela condição, podemos varrer um range de altitude e determinar o $ROC_{max}$ para todos os níveis de voo. O teto de serviço de uma aeronave ocorre quando o ROC para aquela condição é de 100 fpm, sendo o teto absoluto quando o $ROC_{max}$ é zero.
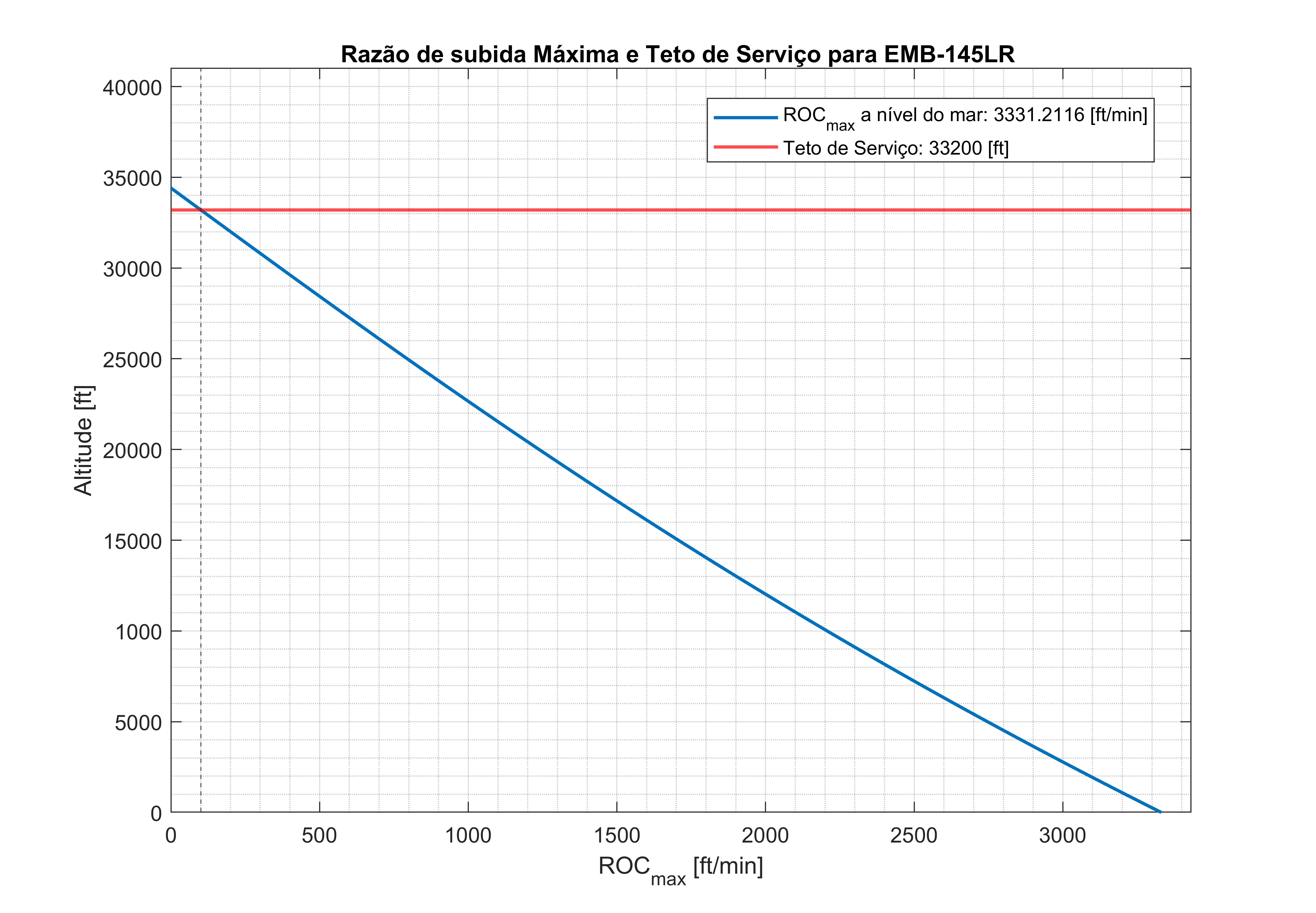$ROC{max}$ vs altitude do EMB-145LR_
Conforme a imagem acima encontramos:
- $ROC_{max} = 3331,21 \text{ [ft/min]}$
- Teto de Serviço de: $33200 \text{ [ft]}$
12 Curvas Polares de Empuxo e Potência
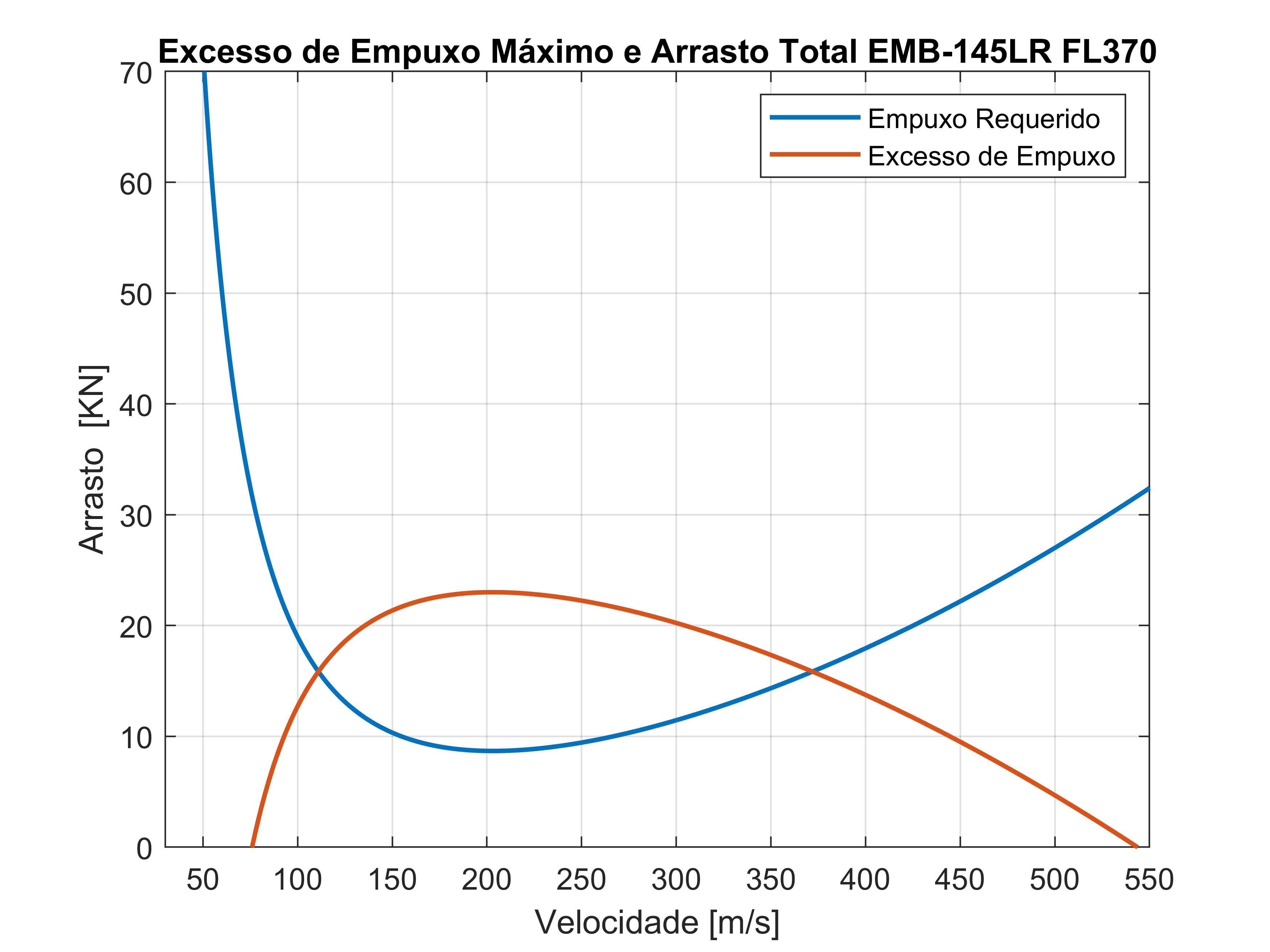
As curvas polares de empuxo relacionam as forças de empuxo requerido e empuxo disponível com a velocidade da aeronave.O conceito de empuxo requerido está associado diretamente com a força que o motor deve empregar para manter a aeronave em voo e corresponde ao arrasto total. O empuxo disponível para aeronaves a jato pode ser aproximado como constante.A figura abaixo mostra o gráfico de excesso de empuxo para EMB-145LR onde a curva de excesso de empuxo é a diferença entre o empuxo disponível e o empuxo requerido, sendo crucial para os cálculos de razão de subida máxima e máximo ângulo de subida da aeronave. Ao determinar os empuxos, e uma vez multiplicados pela velocidade da aeronave, temos as curvas de potência que de fato são usadas para o cálculo de $ROC_{max}$ conforme visto na equação (32).
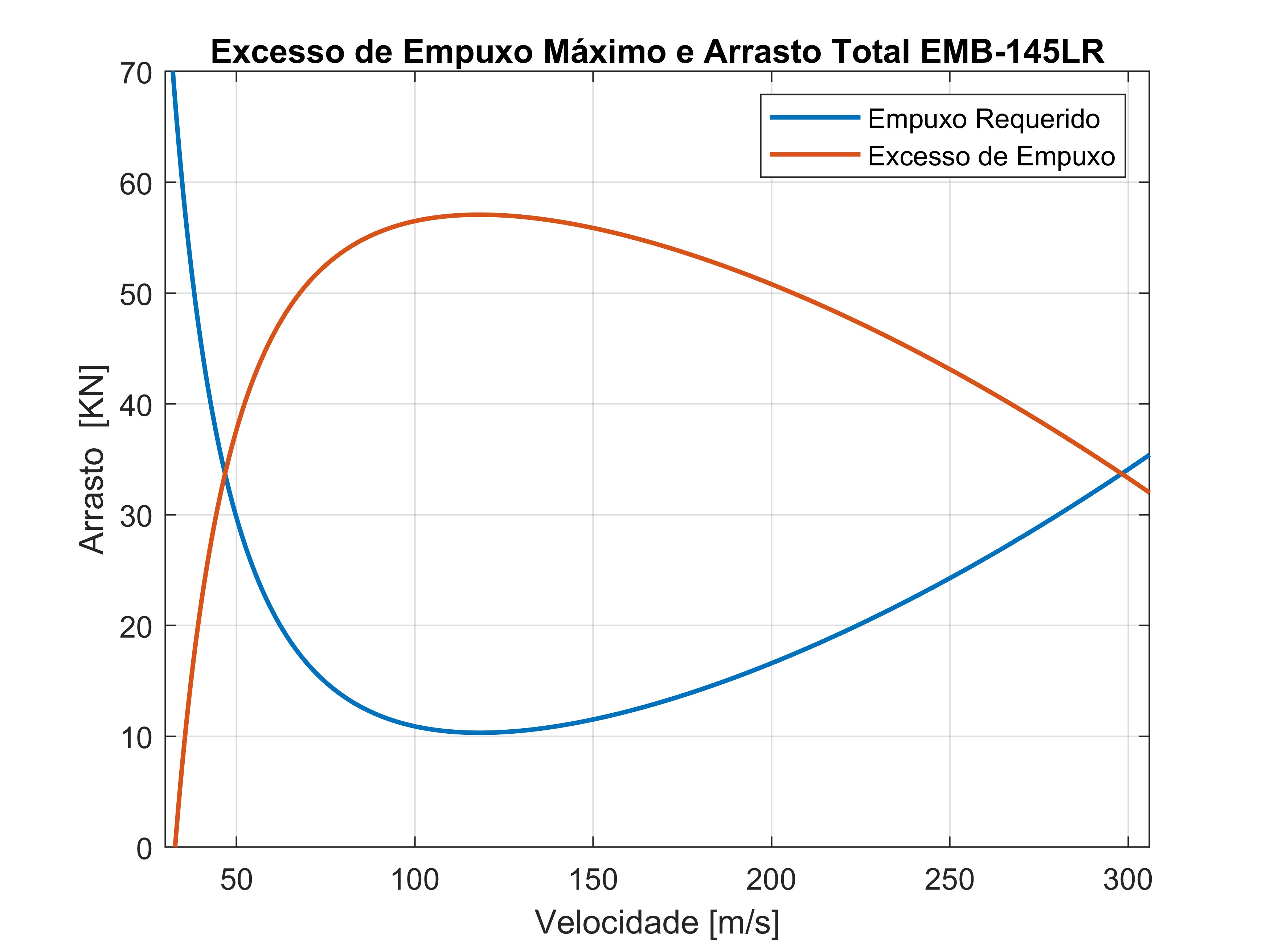Excesso de empuxo máximo e arrasto total
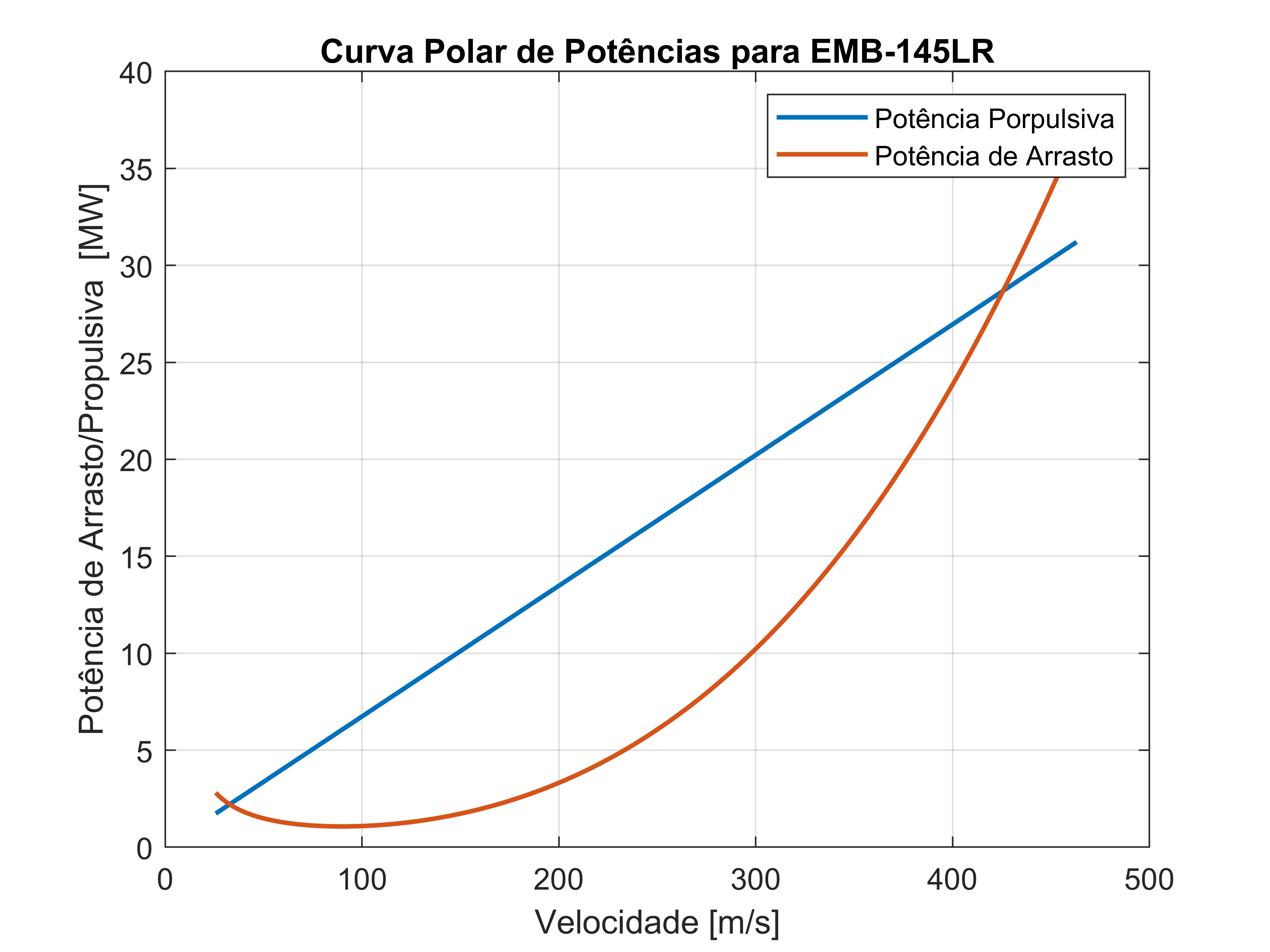
Curva polar de Potência, usada efetivamente para determinação do $ROC_{max}$:
Polar de Potência EMB-145LR
13. Máximo Ângulo de Subida ($\gamma_{max}$)
Podemos determinar o máximo ângulo de subida diretamente pela equação abaixo:
\[\gamma_{\max} = \sin^{-1} \left( \frac{1}{W} \left[ T_{\max} - \frac{1}{2} \rho S (2 C_{D_o}) \left( \frac{2W}{\rho S \sqrt{ \frac{C_{D_o}}{K} }} \right) \right] \right) = \sin^{-1} \left( \frac{1}{W} \left[ T_{\max} - 2W \sqrt{K C_{D_o}} \right] \right)\]Ou ainda podemos usar a polar de empuxo que é referenciada pelo equacionamento abaixo para determinar o $\gamma_{max}$:
\[\gamma_{\max} = \sin^{-1} \left( \frac{T_{\max} - D_{\min}}{W_{\min}} \right)\]Como se trata de uma aeronave de transporte de passageiros e subentende-se que suas missões são sempre com carga e/ou passageiros, para os cálculos usamos o peso como sendo o MTOW da aeronave. Obviamente isso afetará diretamente nos resultados. Para a condição mencionada encontramos:
\[\gamma_{\max} = 15,33^\circ\]14 Comprimento de Pista para Decolagem ($S_{TO}$)
Para determinar o comprimento de pista para decolagem do EMB-145LR precisamos calcular o comprimento necessário em cada trecho:
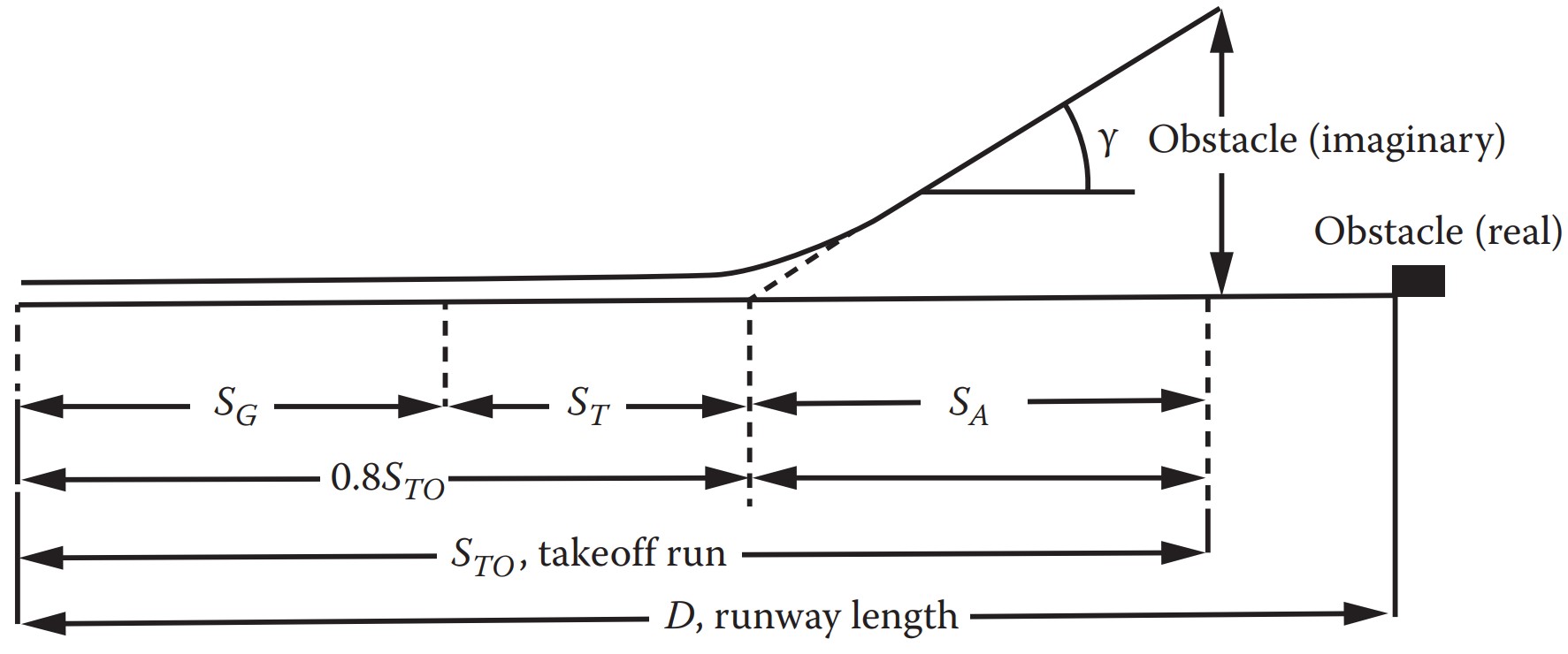Comprimento de pista para decolagem
Onde:
- $S_G$: comprimento de pista em solo, fase de rolagem
- $S_T$: comprimento de pista durante a rotação, fase de transição
- $S_A$: comprimento de pista durante o ganho de altitude, fase aérea
14.1 Velocidade de Mínima Manobrabilidade ($V_{mc}$)
Essa velocidade refere-se à velocidade na qual um dos motores para de funcionar e ocorre uma assimetria de momentos em torno do eixo longitudinal da aeronave. Para compensar essa assimetria é necessário um momento de guinada gerado pelo leme. A $V_{mc}$ é a velocidade mínima que a aeronave precisa estar para a empenagem vertical conseguir gerar força suficiente para anular a assimetria de momentos.
Para determinar a força desse momento na EV usamos:
\[L_{vt} = \frac{T_{left} \cdot l_t}{l_{vt}}\]Onde:
- $T_{left}$: empuxo de apenas um motor (condição OEI)
- $l_t$: distância entre a linha de empuxo do motor e o eixo longitudinal
- $l_{vt}$: distância entre o CG e o centro aerodinâmico da empenagem vertical
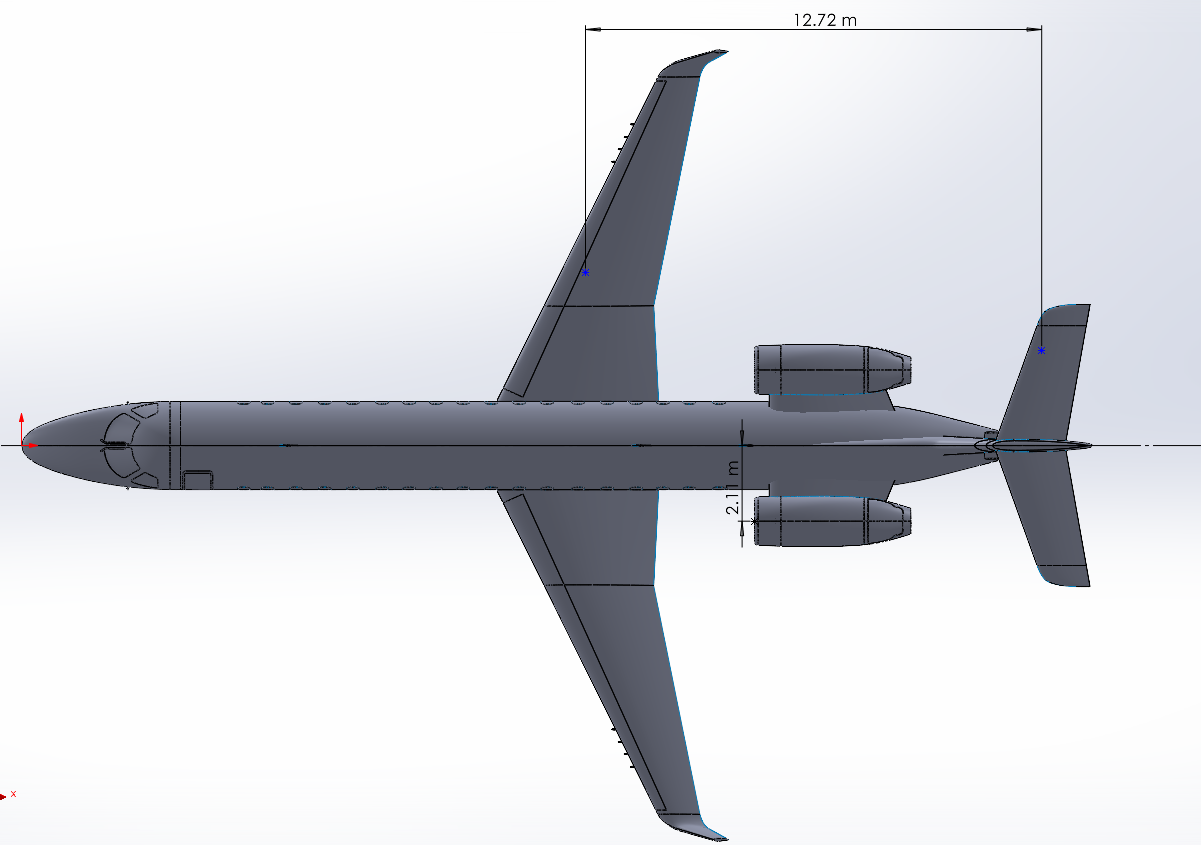Vista superior com as distâncias requeridas
Calculada a força necessária, podemos determinar $V_{mc}$:
\[V_{mc} = \sqrt{ \frac{2 L_{vt}}{\rho S_{vt} C_{L_{max_{vt}}}} }\]Onde:
- $\rho = 1,225 \text{ kg/m}^3$ (massa específica do ar ao nível do mar)
- $S_{vt} = 14,23 \text{ m}^2$ (área da empenagem vertical)
- $C_{L_{max_{vt}}} = 0,9$ (coeficiente máximo de sustentação da EV)
Substituindo os valores:
\[\begin{aligned} V_{mc} &= \sqrt{ \frac{2 \cdot 5590}{1,225 \cdot 14,23 \cdot 0,9} } \\ V_{mc} &= 26,70 \text{ m/s} \end{aligned}\]14.2 Comprimento de Pista na Fase de Rotação ($S_R$)
Para determinar este comprimento:
\[S_R = T_R \cdot V_R\]Onde:
- $T_R = 3 \text{ s}$ (duração de rotação)
- $V_R = 1,05 \cdot V_{mc} = 27,72 \text{ m/s}$
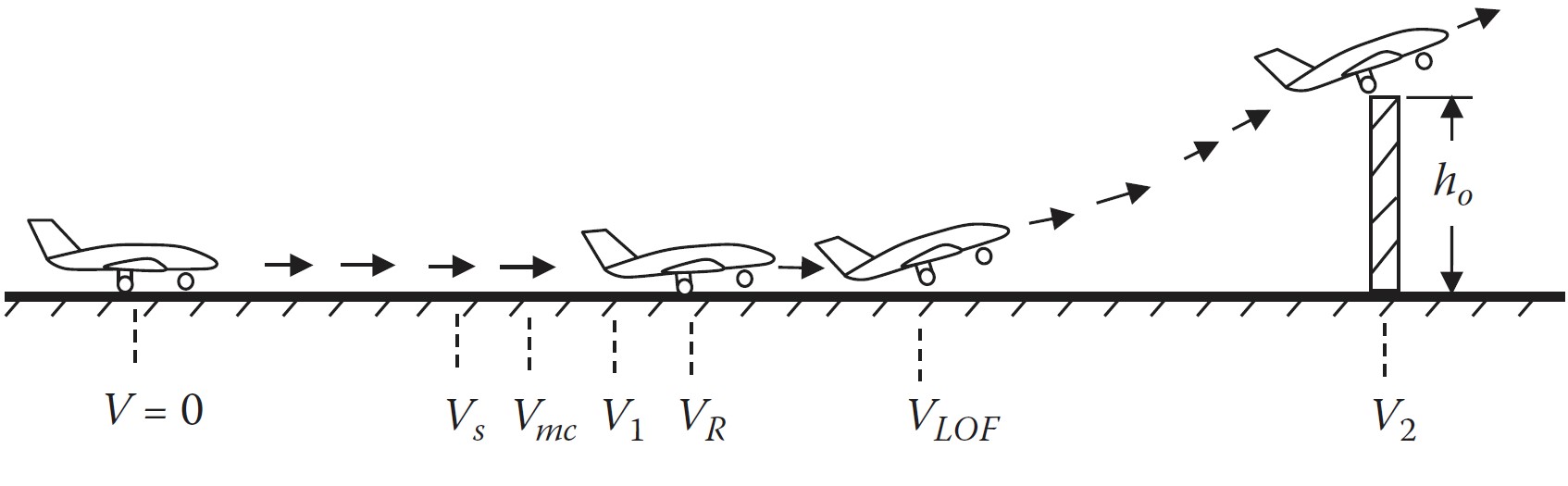Velocidades de referência para rotação
Substituindo os valores:
\[\begin{aligned} S_R &= 3 \cdot 27,72 \\ S_R &= 84,09 \text{ m} \end{aligned}\]14.3 Comprimento de Pista na Fase de Rolagem ($S_G$)
\[S_G = \frac{m}{\rho S (C_{D_{TO}} - \mu C_{L_{TO}})} \ln \left[ \frac{ \left( \frac{T}{mg} \right) - \mu }{ \left( \frac{T}{mg} - \mu \right) - \frac{K_{LO}^2 (C_{D_{TO}} - \mu C_{L_{TO}})}{C_{L_{max}}} } \right]\]Onde:
- $\mu = 0,03$ (coeficiente de fricção para asfalto)
- $C_{D_{TO}} = 0,1215$
- $C_{L_{max}} = 2,2$
- $K_{LO} = 1,1$
- $S = 51,18 \text{ m}^2$
- $T = 33700 \text{ N}$
Substituindo os valores:
\[\begin{aligned} S_G &= \frac{22000}{1,225 \cdot 51,18 \cdot 0,1215} \ln \left[ \frac{0,3122 - 0,030}{(0,3122 - 0,030) - \frac{1,1^2 \cdot 0,1245}{2,2}} \right] \\ S_G &= 835 \text{ m} \end{aligned}\]14.4 Comprimento de Pista na Fase Aérea ($S_A$)
\[S_A' = \frac{mg}{T_{ab} - D_{ab}} \left[ \frac{V_2^2 - V_{LO}^2}{2g} + h_o \right]\]Onde:
- $T_{ab} = 0,9 \cdot T_{max} = 60660 \text{ N}$
- $D_{ab} = 36829,36 \text{ N}$
- $V_2 = 72,72 \text{ m/s}$
- $V_{LO} = 67,12 \text{ m/s}$
- $h_o = 10,66 \text{ m}$
Substituindo os valores:
\[\begin{aligned} S_A' &= \frac{22000 \cdot 9,81}{60660 - 36829,36} \left[ \frac{72,72^2 - 67,12^2}{2 \cdot 9,81} + 10,66 \right] \\ S_A' &= 457,50 \text{ m} \end{aligned}\]Para a distância final:
\[\begin{aligned} S_A &= \sqrt{ S_A'^2 - h_o^2 } \\ S_A &= 457,38 \text{ m} \end{aligned}\]Finalmente com todos os comprimentos de pistas para cada fase calculados, podemos somá-los e obter o comprimento de pista total para decolagem necessário para p EMB-145LR:
\[\begin{aligned} S_{TO} &= S_G + S_R + S_A \\ S_{TO} &= 835 + 83,16 + 454,50 \\ S_{TO} &= 1373,60 \text{ m} \end{aligned}\]15. Discutindo os valores calculados
A seguir apresentamos uma tabela com todos os valores calculados, os valores publicados e as diferenças entre cada um:
Tabela 6- Valores calculados e publicados
| Item | Desempenho | Valor Calculado | Valor Publicado | Diferença (%) |
|---|---|---|---|---|
| 1 | Velocidade Máxima | 953,42 km/h | 833 km/h | 14% |
| 2 | Máximo Alcance | 2.845,97 km | 3.000 km | 5% |
| 3 | Máxima Razão de Subida | 3.331,21 fpm | 3.500 fpm | 5% |
| 4 | Máximo Ângulo de Subida | 15,33° | - | - |
| 5 | Teto Absoluto | 37.000 ft | 33.200 ft | 11% |
| 6 | Pista de Decolagem | 1.373,60 m | 1.970 m | 30% |
| 7 | Máxima Autonomia | 3,8187 h | - | - |
Discussão dos Resultados
Velocidade Máxima
A diferença encontrada na velocidade máxima deve-se ao fato que nossa estimativa não leva em conta o aumento do arrasto da aeronave para os efeitos da compressibilidade do ar em velocidade subsônica, por isso o valor encontrado é ligeiramente maior que o publicado. Sendo que esse já considera o aumento abrupto do arrasto nessa condição de voo.
Máximo Alcance
A diferença encontrada no máximo alcance da aeronave deve-se ao fato que não sabemos qual o método (programa) utilizado para o alcance máximo do fabricante. Também não sabemos qual o peso de combustível queimado adotado pelo fabricante, além disso nosso arrasto parasita para condição de cruzeiro é uma estimativa, e portanto devem haver discrepâncias com o valor utilizado pela fabricante, impactando diretamente no resultado final.
Máxima Razão de Subida
As discrepâncias na máxima razão de subida podem ser atribuídas às imperfeições observadas na curva de excesso de empuxo da aeronave que determinamos, ao serem comparadas com as curvas fornecidas pelo fabricante.
Máximo Ângulo de Subida
Não encontramos dados disponíveis para essa variável, porém nosso cálculo foi feito de forma direta podendo haver diferenças com valores oficiais não divulgados.
Teto Absoluto
Nossos cálculos de teto absoluto levam em consideração um limite máximo de razão de subida de 100 fpm. Como há discrepâncias no cálculo do ROC máximo, temos um erro associado ao cálculo do teto de serviço da aeronave quando comparado com o valor publicado.
Pista de Decolagem
Esse parâmetro é o que apresentou maior variação de erro percentual, uma vez que inúmeras variáveis influenciam no seu cálculo, até mesmo dentro do material disponível na internet há variações para esse comprimento de pista durante a decolagem. Seu erro pode estar associado ao coeficiente máximo que adotamos com base em dados empíricos, uma vez que não sabemos o valor oficial, condições da pista, vento, temperatura, arrasto do flap, dentre outros. Mesmo com a diferença, o valor encontrado é razoável com os dados que temos estimados.
Máxima Autonomia
O valor encontrado é condizente com os parâmetros que adotamos para o cálculo, e dentro do esperado. Não encontramos valores de máxima autonomia disponíveis para essa aeronave na internet.
16. Proposta de Plano de Voo
Nessa seção iremos propor um voo entre as cidades de Uberlândia-Minas Gerais e Boa Vista-Roraima. A aeronave utilizada é a mesma que usamos durante todo o escopo desse trabalho, o EMB-145LR. O voo irá transportando 50 passageiros e 1.400 kg de carga. O nível de voo é o FL370. O aeroporto alternativo está localizado na cidade de Manaus que dista 698 km de Boa Vista. Manaus é o candidato mais próximo com aeroporto adequado para a rota alternada nesse voo.
O plano de voo foi gerado através do site Simbrief onde podemos gerar um plano de voo mais próximo possível do real. O plano de voo completo encontra-se nos anexos desse trabalho, lá temos todas as informações em detalhes, como todas as informações trecho a trecho, aerovia usada, cartas de saída (SID) e de aproximação (IAC) que são utilizadas pelos pilotos.
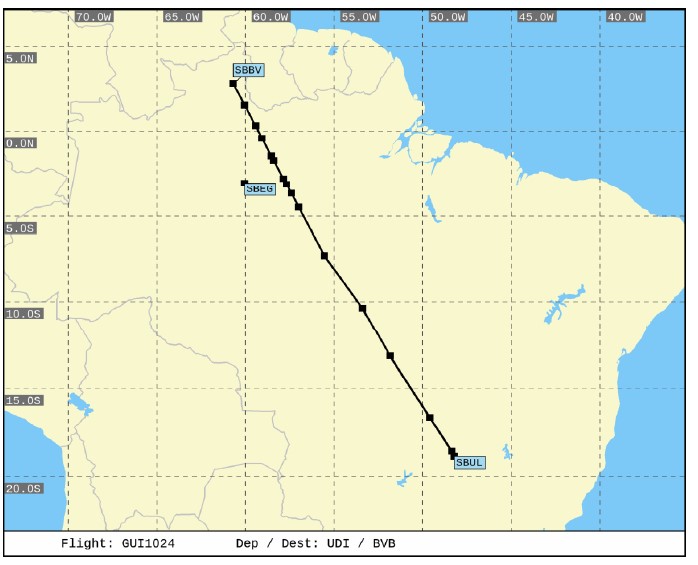Rota proposta entre Uberlândia-MG e Boa Vista-RR
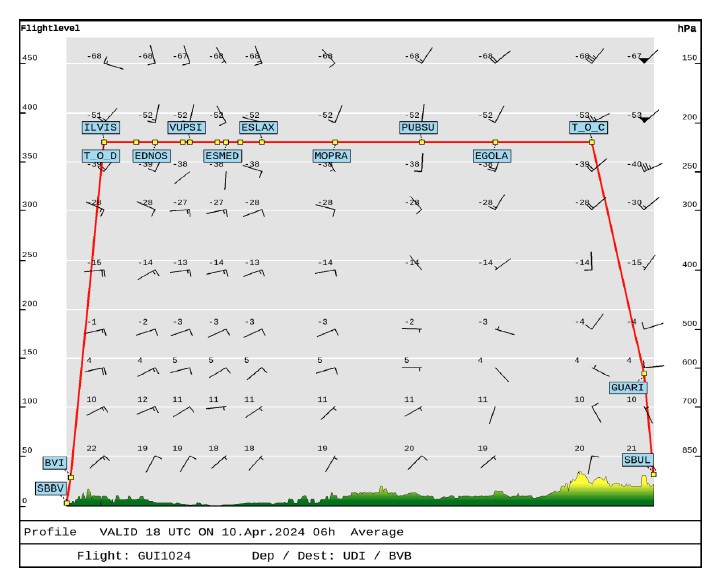Missão completa para o voo proposto, e os perfis de vento em diferentes altitudes
Para o voo em questão temos as seguintes informações:
- Peso Máximo de Decolagem Estimado (TOW): 19.242 kg
- Peso de Combustível Declarado (TFW): 1.479 kg
- Peso Vazio Operacional (OEW): 12.114 kg
- Consumo Específico do Motor para voo de Cruzeiro (TSFC): 1,845 × 10⁻⁵ kg/N·s
- Distância de Voo Desejada (R): 2.808 km
- Nível de Voo de Cruzeiro (FL): FL370 (0,3483 kg/m³)
- Velocidade em Voo de Cruzeiro (V₀): 230,0 m/s
- Reserva Técnica: 10% tempo de voo + 185 km (alternativo) + 45 min de espera
Determinando o Alcance para o Voo
Primeiro determinamos o peso em voo de cruzeiro pela relação abaixo:
\[W_{cruise} = \frac{2W_0 - W_{fuel}}{2}\]Considerando:
- $W_0 = \text{TOW}$
- $W_{fuel} = \text{TFW}$
Substituindo os valores:
\[\begin{aligned} W_{cruise} &= \frac{2 \cdot 19.242 - 1.479}{2} \\ W_{cruise} &= 181.509,52 \text{ N} \end{aligned}\]Com o peso em voo de cruzeiro calculado, podemos determinar o coeficiente de sustentação para essa etapa do voo:
\[C_{L_{cruise}} = \frac{2 \cdot W_{cruise}}{\rho S V_0^2}\]Considerando:
- $\rho = 0,3486 \text{ kg/m}^3$
- $S = 51,18 \text{ m}^2$
- $V_0 = 230,00 \text{ m/s}$
Substituindo os valores:
\[\begin{aligned} C_{L_{cruise}} &= \frac{2 \cdot 181.509,52}{0,3483 \cdot 51,18 \cdot 230^2} \\ C_{L_{cruise}} &= 0,385 \end{aligned}\]Determinado o coeficiente de sustentação para o voo em cruzeiro, podemos encontrar a eficiência aerodinâmica:
\[\left( \frac{L}{D} \right)_{cruise} = \frac{1}{ \frac{C_{D_0}}{C_{L_{cruise}}} + K C_{L_{cruise}} }\]Considerando:
- $C_{D_0} = 0,0188$
- $K = 0,0485$
Substituindo os valores:
\[\left( \frac{L}{D} \right)_{cruise} = 14,81\]Para descobrir a relação de pesos na fase de cruzeiro:
\[\frac{W_3}{W_2} = e^{ -\frac{g \cdot R \cdot TSFC}{V_0 (L/D)_{cruise}} }\]Considerando:
- $g = 9,81 \text{ m/s}^2$
- $R = 2.808 \times 10^6 \text{ m}$
- $TSFC_{cruise} = 1,845 \times 10^{-5} \text{ kg/N·s}$
- $V_0 = 230 \text{ m/s}$
- $(L/D)_{cruise} = 14,81$
Substituindo os valores:
\[\frac{W_3}{W_2} = 0,86125\]Finalmente, o alcance total:
\[R_{total} = -\frac{V_0 \ln \left( \frac{W_3}{W_2} \right) \left( \frac{L}{D} \right)_{cruise}}{g \cdot TSFC_{cruise}}\]Substituindo os valores:
\[R_{total} = 2.808 \text{ km}\]Os valores encontrados para o alcance calculado e para o plano de voo batem perfeitamente.
Determinando o Tempo de Voo
Para encontrar o tempo de voo usamos:
\[t_{voo} = \frac{R}{V_0}\]Substituindo os valores:
\[\begin{aligned} t_{flight} &= \frac{2.808}{828} \\ t_{flight} &= 3,40 \text{ h} \end{aligned}\]O valor encontrado é bem próximo ao plano de voo que informa um tempo de 3,57 h.
Polar de Empuxo e Potência em Nível do Mar
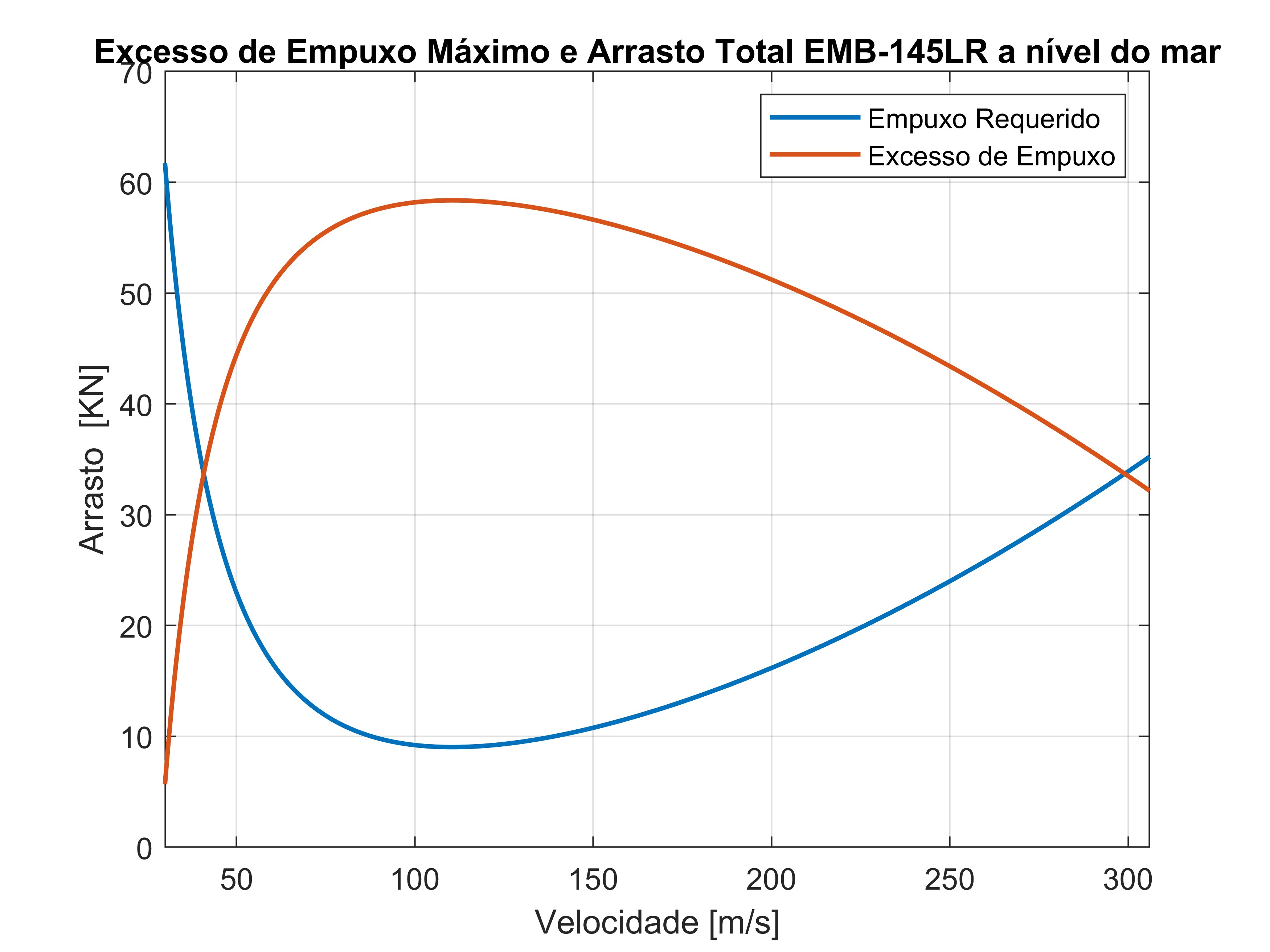Polar de empuxo a nível do mar
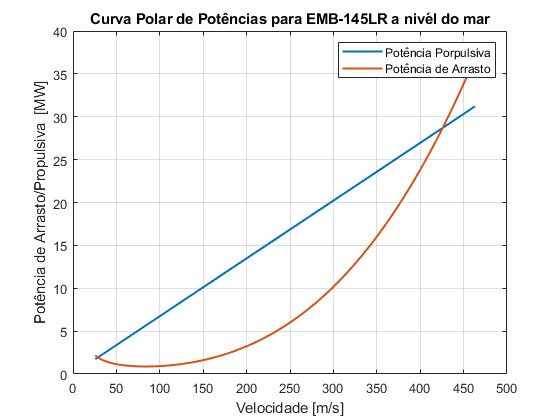Polar de potência a nível do mar
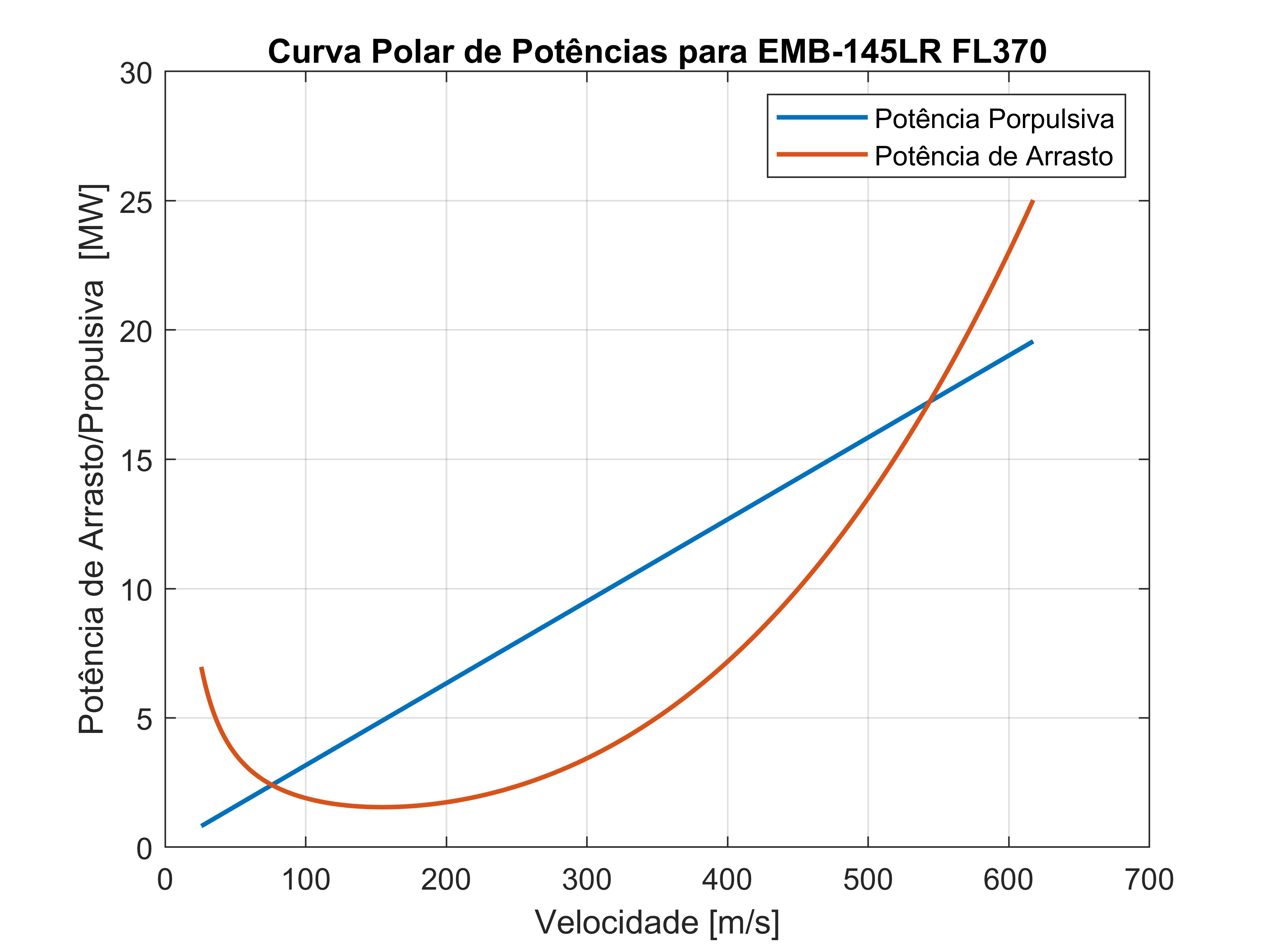
Polar de Empuxo e Potência em Altitude de Cruzeiro (FL370)
Polar de Empuxo a FL370
Polar de Potência a FL370
Referências
SADRAEY, M. H Aircraft performance: An Engineering Approach. CRC Press,2017. ↩︎ ↩︎2
Estimating the Oswald factor from basic aircraft geometrical parameters- Mihaela and Scholz, Dieter ↩︎
RAYMER, D. Aircraft Design: a conceptual approach. American Institute and Astronautics, Incs,2012 ↩︎
Airport Planning Manual EMB-145, 2019 ↩︎